题目内容
【题目】如图,已知抛物线y=ax2+4x+c经过A(2,0)、B(0,﹣6)两点,其对称轴与x轴交于点C.
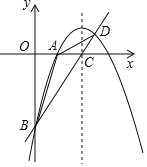
(1)求该抛物线和直线BC的解析式;
(2)设抛物线与直线BC相交于点D,求△ABD的面积;
(3)在该抛物线的对称轴上是否存在点Q,使得△QAB的周长最小?若存在,求出Q点的坐标及△QAB最小周长;若不存在,请说明理由.
【答案】(1)y=﹣![]() x2+4x﹣6,y=
x2+4x﹣6,y=![]() x﹣6;(2)
x﹣6;(2)![]() ;(3)存在点Q的坐标(4,﹣2)时,使得△QAB的周长最小.
;(3)存在点Q的坐标(4,﹣2)时,使得△QAB的周长最小.
【解析】
(1)将点A、点B的坐标代入可得出抛物线的解析式,从而得出点C的坐标,然后利用待定系数法求出直线BC的解析式;
(2)求出点D的坐标,然后根据S△ABD=S△ACD+S△ABC进行计算,即可得出答案;
(3)AB长度固定,只需满足QA+QB最小即可,找点A关于对称轴的对称点A',连接A'B,则A'B与对称轴的交点即是点Q的位置,求出直线A'B的解析式,即可解决问题.
解:(1)将A(2,0)、B(0,﹣6)代入抛物线解析式得:![]() ,
,
解得: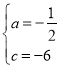 ,
,
故抛物线的解析式为:y=﹣![]() x2+4x﹣6,
x2+4x﹣6,
其对称轴为:x=4,
故点C的坐标为(4,0),
设直线BC的解析式为y=kx+b,将点B、点C的坐标代入可得:![]() ,
,
解得: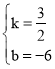 ,
,
故直线BC的解析式为y=![]() x﹣6;
x﹣6;
(2)联立直线BC与抛物线的解析式得: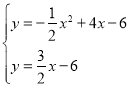 ,
,
解得:![]() 或
或![]() ,
,
故点D的坐标为(5,![]() ),
),
则S△ABD=S△ACD+S△ABC=![]() ;
;
(3)点A关于抛物线对称轴的对称点为A',连接A'B,则A'B与对称轴的交点即是点Q的位置:
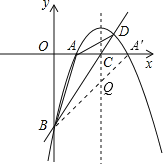
由题意得:A'坐标为(6,0),B(0,﹣6),
设直线A'B的解析式为:y=mx+n,代入两点坐标可得:![]() ,
,
解得:![]() ,
,
即直线A'B的解析式为y=x﹣6,
当x=4时,y=4﹣6=-2,
故点Q的坐标为(4,﹣2).
即存在点Q的坐标(4,﹣2)时,使得△QAB的周长最小.

【题目】某超市销售一种商品,成本每千克40元,规定每千克售价不低于成本,且不高于80元,经市场调查,每天的销售量y(千克)与每千克售价x(元)满足一次函数关系,部分数据如下表:
售价x(元/千克) | 50 | 60 | 70 |
销售量y(千克) | 100 | 80 | 60 |
(1)求y与x之间的函数表达式;
(2)设商品每天的总利润为W(元),则当售价x定为多少元时,厂商每天能获得最大利润?最大利润是多少?
(3)如果超市要获得每天不低于1350元的利润,且符合超市自己的规定,那么该商品每千克售价的取值范围是多少?请说明理由.
【题目】九(1)班数学兴趣小组经过市场调查,整理出某种商品在第x(1≤x≤90)天的售价与销售量的相关信息如下表:
时间x(天) | 1≤x<50 | 50≤x≤90 |
售价(元/件) | x+40 | 90 |
每天销量(件) | 200-2x | |
已知该商品的进价为每件30元,设销售该商品的每天利润为y元[
(1)求出y与x的函数关系式;
(2)问销售该商品第几天时,当天销售利润最大,最大利润是多少?
(3)该商品在销售过程中,共有多少天每天销售利润不低于4800元?请直接写出结果.