题目内容
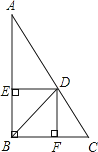
【题目】如图,在数学活动课中,小敏为了测量校园内旗杆CD的高度,先在教学楼的底端A点处,观测到旗杆顶端C的仰角∠CAD=60°,然后爬到教学楼上的B处,观测到旗杆底端D的俯角是30°,已知教学楼AB高4米.
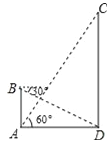
(1)求教学楼与旗杆的水平距离AD;(结果保留根号)
(2)求旗杆CD的高度.
【答案】(1)4![]() m;(2)12m.
m;(2)12m.
【解析】
试题分析:(1)根据题意得出∠ADB=30°,进而利用锐角三角函数关系得出AD的长;(2)利用(1)中所求,结合CD=ADtan60°求出答案.
试题解析:(1)∵教学楼B点处观测到旗杆底端D的俯角是30°, ∴∠ADB=30°,
在Rt△ABD中,∠BAD=90°,∠ADB=30°,AB=4m, ∴AD=![]() =
=![]() =4
=4![]() (m),
(m),
答:教学楼与旗杆的水平距离是4![]() m;
m;
(2)∵在Rt△ACD中,∠ADC=90°,∠CAD=60°,AD=4![]() m,
m,
∴CD=ADtan60°=4![]() ×
×![]() =12(m),
=12(m),
答:旗杆CD的高度是12m.

【题目】某校组织了九年级学生英语口语模拟测试,现从中随机抽取部分学生的口语模拟测试成绩统计如下.
口语成绩(分) | 人数(人) | 百分比(%) |
26 | 8 | 16 |
27 | 24 | |
28 | 15 | |
29 | m | |
30 | 5 |
根据上面提供的信息,回答下列问题:
(1)扇形统计图中的圆心角a= °;
(2)统计表中样本容量m= ;
(3)已知该校九年级共有400名学生,如果口语成绩达28分以上(含28分)为优秀,请估计该校九年级学生口语成绩达到优秀的总人数 
【题目】李明对某校九年级(2)班进行了一次社会实践活动调查,从调查的内容中抽出两项.
调查一:对小聪、小亮两位同学的毕业成绩进行调查,其中毕业成绩按综合素质、考试成绩、体育测试三项进行计算,计算的方法按4:4:2进行,毕业成绩达80分以上为“优秀毕业生”,小聪、小亮的三项成绩如右表:(单位:分)
综合素质 | 考试成绩 | 体育测试 | |
满分 | 100 | 100 | 100 |
小聪 | 72 | 98 | 60 |
小亮 | 90 | 75 | 95 |
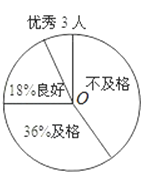
调查二:对九年级(2)班50名同学某项跑步成绩进行调查,并绘制了一个不完整的扇形统计图,请你根据以上提供的信息,解答下列问题:
(1)小聪和小亮谁能达到“优秀毕业生”水平?哪位同学的毕业成绩更好些?
(2)升入高中后,请你对他俩今后的发展给每人提一条建议.
(3)扇形统计图中“优秀率”是多少?
(4)“不及格”在扇形统计图中所占的圆心角是多少度?