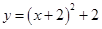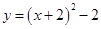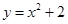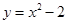题目内容
如图,已知△OAB的顶点A(-6,0),B(0,2),O是坐标原点, 将△OAB绕点O按顺时针旋转90°,得到△ODC.
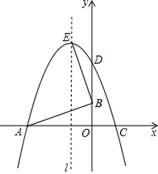
(1)写出C点的坐标为 ;
(2)设过A,D,C三点的抛物线的解析式为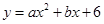 ,求其解析式?
,求其解析式?
(3)证明AB⊥BE.

(1)写出C点的坐标为 ;
(2)设过A,D,C三点的抛物线的解析式为
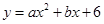 ,求其解析式?
,求其解析式?(3)证明AB⊥BE.
(1)C(2,0),D(0,6);(2)y=﹣ x2﹣2x+6;(3)证明见解析.
x2﹣2x+6;(3)证明见解析.
 x2﹣2x+6;(3)证明见解析.
x2﹣2x+6;(3)证明见解析.试题分析:(1)根据旋转的性质,可得OC=OB,OD=OA,进而可得C、D两点的坐标;
(2)由于抛物线过点A(﹣6,0),C(2,0),所以设抛物线的解析式为y=a(x+6)(x﹣2)(a≠0),再将D(0,6)代入,求出a的值,得出抛物线的解析式,然后利用配方法求出顶点E的坐标;
(3)已知A、B、E三点的坐标,运用两点间的距离公式计算得出AB2=40,BE2=40,AE2=80,则AB2+BE2=AE2,根据勾股定理的逆定理即可证明AB⊥BE.
试题解析:(1)∵将△OAB绕点O按顺时针旋转90°,得到△ODC,
∴△ODC≌△OAB,
∴OC=OB=2,OD=OA=6,
∴C(2,0),D(0,6);
(2)∵抛物线过点A(﹣6,0),C(2,0),
∴可设抛物线的解析式为y=a(x+6)(x﹣2)(a≠0),
∵D(0,6)在抛物线上,
∴6=﹣12a,
解得a=﹣
 ,
,∴抛物线的解析式为y=﹣
 (x+6)(x﹣2),即y=﹣
(x+6)(x﹣2),即y=﹣ x2﹣2x+6;
x2﹣2x+6;(3)∵y=﹣
 x2﹣2x+6=﹣
x2﹣2x+6=﹣ (x+2)2+8,
(x+2)2+8,∴顶点E的坐标为(﹣2,8),
连接AE.
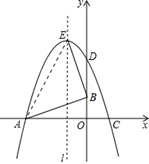
∵A(﹣6,0),B(0,2),E(﹣2,8),
∴AB2=62+22=40,BE2=(﹣2﹣0)2+(8﹣2)2=40,AE2=(﹣2+6)2+(8﹣0)2=80,
∴AB2+BE2=AE2,
∴AB⊥BE..

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案
相关题目
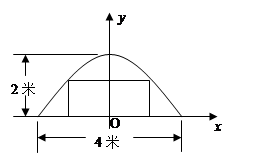
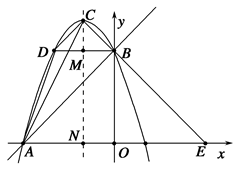
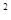 +4x+5交x轴于A、B(以A左B右)两点,交y轴于点C.
+4x+5交x轴于A、B(以A左B右)两点,交y轴于点C.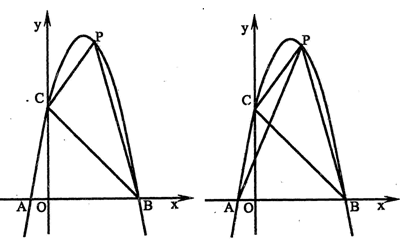
 x2+bx+c的图象经过B、C两点.
x2+bx+c的图象经过B、C两点.
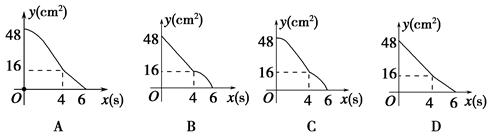
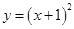 向下平移2个单位,再向右平移1个单位,所得到的抛物线是( )
向下平移2个单位,再向右平移1个单位,所得到的抛物线是( )