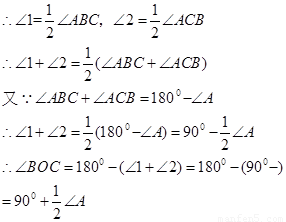Question

认真阅读下面关于三角形内外角平分线所夹角的探究片段，完成所提出的问题.

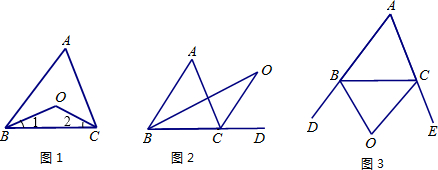
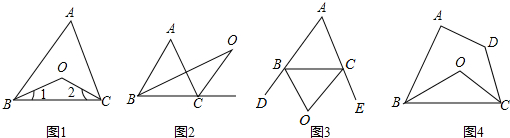
探究1：如图1，在中，是与的平分线和的交点，分析发现,理由如下: ∵和分别是，的角平分线

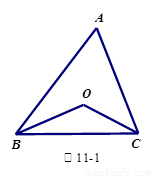
（1）探究2：如图2中, 是与外角的平分线和的交点，试分析与有怎样的关系？请说明理由.

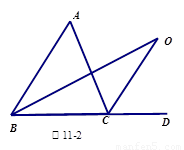
（2）探究3： 如图3中，是外角与外角的平分线和的交点，则与有怎样的关系？（直接写出结论）

（3）拓展:如图4，在四边形ABCD中，O是∠ABC与∠DCB的平分线BO和CO的交点，则∠BOC与∠A+∠D有怎样的关系？（直接写出结论）

（4）运用：如图5，五边形ABCDE中，∠BCD、∠EDC的外角分别是∠FCD、∠GDC，CP、DP分别平分∠FCD和∠GDC且相交于点P，若∠A=140°，∠B=120°，∠E=90°，则∠CPD=_____度．

 

Answer 1

【答案】

（1）∠BOC=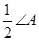；（2）∠BOC=90°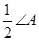－；（3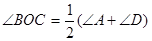）；（4）95°

【解析】

试题分析：根据角平分线的性质及三角形外角的性质求解即可，注意解本题要有整体意识.

（1）探究2结论：∠BOC=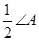

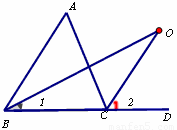
理由如下：

∵BO和CO分别是∠ABC和∠ACD的角平分线

 

；

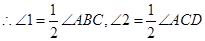
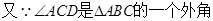
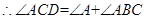
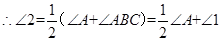
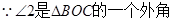
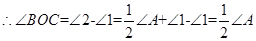（2）探究3：结论∠BOC=90°－；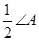

（3）拓展：结论；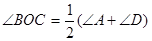

（4）运用：95°.

考点：角平分线的性质，三角形外角的性质

点评：角平分线的性质是初中数学的重点，贯穿于整个初中数学的学习，是中考中比较常见的知识点，一般难度不大，需熟练掌握.