题目内容
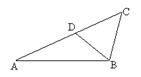
如图,△ABC中,AB=AC,点E是AC上一点,ED⊥BC于点D,DE的延长线交BA的延长线于点F。
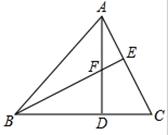
求证:△AEF是等腰三角形

求证:△AEF是等腰三角形
证明:△ABC中,AB=AC,即∠B=∠C,又ED⊥BC,所以∠BDF=∠CDE,所以△BDF∽△CDE,所以∠F=∠CED,又因为对顶角相等,所以∠CED=∠AEF,所以∠AEF=∠F,所以AF=AE,即△AEF是等腰三角形。
试题分析:先通过求出两个三角形有两组角相等,证明出这两个三角形相似,再有对顶角相等,进行等量代换,从而证明等腰三角形。
点评:相似三角形的判断条件为两组角相等,而对顶角原则则是两条直线相交,其交点所对应的两组角对顶相等。

练习册系列答案
相关题目
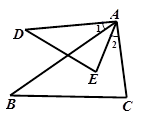
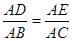
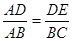
 =
=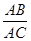 ; (B)
; (B) =
=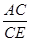 ;
; =
=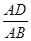 ; (D)
; (D) .
.
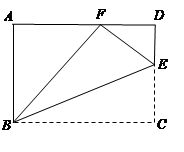
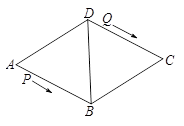
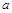 cm/s,经过3秒后,P、Q分别到达E、F两点,若△BEF与问题(2)中的△AMN相似,试求
cm/s,经过3秒后,P、Q分别到达E、F两点,若△BEF与问题(2)中的△AMN相似,试求