题目内容
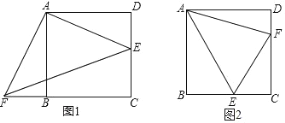
【题目】如图1,四边形ABCD是正方形,△ADE经旋转后与△ABF重合.
(1)旋转中心是 ;旋转角是 度; 如果连接EF,那么△AEF是 三角形.
(2)用上述思想或其他方法证明:如图2,在正方形ABCD中,点E、F分别在BC、CD上,且∠EAF=45°.
求证:EF=BE+DF.
(3)若DF=4,EF=10,求四边形AECD的面积。
【答案】(1)△AEF是等腰直角三角形(2)证明见解析(3)108
【解析】试题分析:(1)△ADE经旋转后与△ABF重合,所以旋转中心为点A,因为四边形ABCD是正方形,所以∠BAD=90°,所以旋转角为90°,由旋转得AE=AF,所以△AEF是等腰直角三角形;(2)利用第一问的旋转的思想来证明即可;(3)根据第二问的结论,可以求出正方形的边长,从而求出正方形的面积.
试题解析:
(1)旋转中心是点A,旋转角=∠DAB=90°,△AEF是等腰直角三角形;
(2)如图所示,将△ABE绕A点逆时针旋转90°,得到△ADE′,
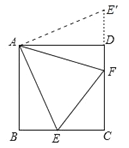
因为∠EAF=45°,
所以∠BAE+∠DAF=45°,
因为∠BAE=∠DAE′,
所以∠FAE′=45°,
所以∠FAE′=∠FAE,
因为∠ADE′=∠ADF=90°,
所以E'、D、F三点共线,
又因为AF=AF,AE=AE′,
所以△EAF≌△E′AF(SAS),
所以EF=E′F,
因为E′F=DF+DE′,E′D=BE,
所以EF=BE+DF.
(3)108

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目