Question

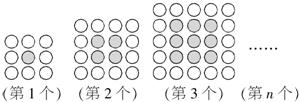
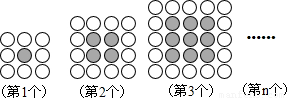
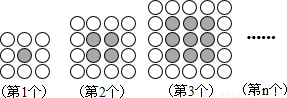
用同样大小的黑、白两种颜色的棋子摆设如图所示的正方形图案．

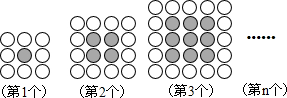
则第4个图案中白色棋子

20

枚，第n（n是正整数）个图案中白色棋子

4（n+1）

枚（用含有n的代数式表示）．

Answer 1

分析：此题可以正方形的周长计算公式为基础，分析图形规律，得出结论，然后代入数值求解即可．

解答：解：第1个正方形图案有棋子共3²=9枚，其中黑色棋子有1²=1枚，白色棋子有（3²-1²）枚；
第2个正方形图案有棋子共4²=16枚，其中黑色棋子有2²=4枚，白色棋子有（4²-2²）枚；
…由此可推出想第n个图案的白色棋子数为（n+2）²-n²=4（n+1）．
故第n个图案的白色棋子数为（n+2）²-n²=4（n+1），
当n=4时，4×（4+1）=20．
故答案为：20，4n+4．

点评：本题考查了图形的变化类问题，根据图形提供的信息探索规律，是近几年较流行的一种探索规律型问题．解决这类问题首先要从简单图形入手，抓住随着“编号”或“序号”增加时，后一个图形与前一个图形相比，在数量上增加（或倍数）情况的变化，找出数量上的变化规律，从而推出一般性的结论．