题目内容
如果a、b是整数,且x2+x-1是ax3+bx+1的因式,则b的值为______.
设ax3+bx+1=(mx-1)(x2+x-1).
∵(mx-1)(x2+x-1)=mx3+(m-1)x2+(-m-1)x+1,
∴ax3+bx+1=mx3+(m-1)x2+(-m-1)x+1,
比较两边对应项系数,得
,
解得
.
则b的值为-2.
故答案为-2.
∵(mx-1)(x2+x-1)=mx3+(m-1)x2+(-m-1)x+1,
∴ax3+bx+1=mx3+(m-1)x2+(-m-1)x+1,
比较两边对应项系数,得
|
解得
|
则b的值为-2.
故答案为-2.

练习册系列答案
相关题目
 是无理数,而无理数是无限不循环小数,因此
是无理数,而无理数是无限不循环小数,因此 来表示
来表示 ,即
,即 ,
, 的整数部分为2,小数部分为
的整数部分为2,小数部分为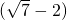 .
. 的整数部分为a,那么a=________.如果
的整数部分为a,那么a=________.如果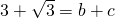 ,其中b是整数,且0<c<1,那么b=________,c=________.
,其中b是整数,且0<c<1,那么b=________,c=________.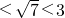 ,所以
,所以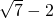 ).
). 的整数部分为a,那a=______.如果
的整数部分为a,那a=______.如果