题目内容
如图，一个圆形转盘被等分成七个扇形区域，上面分别标有数字1、2、3、4、5、6、7，转盘指针的位置固定，转动转盘后自由停止．转动转盘一次，当转盘停止转到时，记指针指向标有偶数所在区域的概率为P（偶数），指针指向标有奇数所有区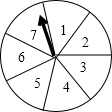
域的概率为P（奇数），则P（偶数）与P（奇数）的大小关系是（ ）
域的概率为P（奇数），则P（偶数）与P（奇数）的大小关系是（ ）| A、P（偶数）＞P（奇数） | B、P（偶数）=P（奇数） | C、P（偶数）＜P（奇数） | D、P（偶数）≤P（奇数） |
分析：先分别求出偶数、奇数在整个转盘中所占面积的比值，根据此比值进行比较即可解答．
解答：解：∵转盘等分成7个扇形，其中偶数占3份，奇数占4份，
∴指针指向标有偶数所在区域的概率为P（偶数）=
，
指针指向标有奇数所有区域的概率为P（奇数）=
，
所以P（偶数）＜P（奇数）．
故选C．
∴指针指向标有偶数所在区域的概率为P（偶数）=
| 3 |
| 7 |
指针指向标有奇数所有区域的概率为P（奇数）=
| 4 |
| 7 |
所以P（偶数）＜P（奇数）．
故选C．
点评：本题将概率的求解设置于转动转盘游戏中，考查学生对简单几何概型的掌握情况，既避免了单纯依靠公式机械计算的做法，又体现了数学知识在现实生活、甚至娱乐中的运用，体现了数学学科的基础性．用到的知识点为：概率=相应的面积与总面积之比．
练习册系列答案
名校课堂系列答案
相关题目
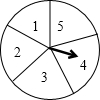如图，一个圆形转盘被等分成五个扇形区域，上面分别标有数字1，2，3，4，5，转盘指针的位置固定，转动转盘后任其自由停止．转动转盘一次，当转盘停止转动时，记指针指向标有偶数所在区域的概率为P（偶数），指针指向标有奇数所在区域的概率为P（奇数），则P（偶数）
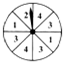15、如图，一个圆形转盘被等分成八个扇形区域，上面分别标有数字1、2、3、4，转盘指针的位置固定，转动转盘后任其自由停止．转动转盘一次，当转盘停止转动时，记指针指向标有“3”所在区域的概率为P（3），指针指向标有“4”所在区域的概率为P（4），则P（3）
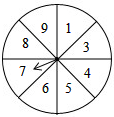如图，一个圆形转盘被等分成八个扇形区域，上面分别标上1，3，4，5，6，7，8，9，转盘可以自由转动，转动转盘一次，指针指向的数字为偶数所在区域的概率是（ ）