题目内容
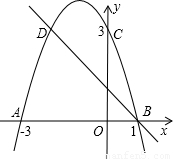
如图,二次函数的图象与x轴相交于A(-3,0),B(1,0)两点,与y轴相交于点C(0,3),点C、D是二次函数图象上的一对对称点.一次函的图象过点B、D.(1)求D点的坐标.
(2)求一次函数的表达式.
(3)根据图象写出使一次函数值大于二次函数值的x的取值范围.
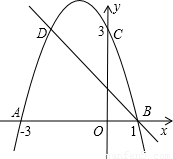
【答案】分析:(1)利用点C、D是二次函数图象上的一对对称点,可得出D点的坐标,
(2)运用待定系数法,将D,B点代入求出,
(3)在坐标系中利用x取相同值,比较出对应值的大小,从而确定,两函数的大小关系.
解答:解:(1)∵抛物线的对称轴是x=-1,而C、D关于直线x=-1对称
∴D(-2,3)
(2)设一次函数为y=kx+b
∴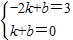 解得
解得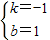 ,∴y=-x+1
,∴y=-x+1
(3)x<-2或x>1
点评:此题主要考查了二次函数的对称性,以及待定系数法求一次函数解析式和利用自变量的取值范围确定函数值大小关系,题目难度不大,非常典型.
(2)运用待定系数法,将D,B点代入求出,
(3)在坐标系中利用x取相同值,比较出对应值的大小,从而确定,两函数的大小关系.
解答:解:(1)∵抛物线的对称轴是x=-1,而C、D关于直线x=-1对称
∴D(-2,3)
(2)设一次函数为y=kx+b
∴
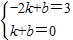 解得
解得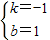 ,∴y=-x+1
,∴y=-x+1(3)x<-2或x>1

点评:此题主要考查了二次函数的对称性,以及待定系数法求一次函数解析式和利用自变量的取值范围确定函数值大小关系,题目难度不大,非常典型.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案
相关题目

 的图象,其顶点坐标为M(1,-4).
的图象,其顶点坐标为M(1,-4).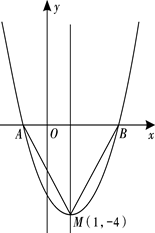
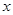 轴的交点A,B的坐标;
轴的交点A,B的坐标; 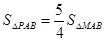 ,若存在,求出P点的坐标;若不存在,请说明理由;
,若存在,求出P点的坐标;若不存在,请说明理由;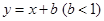 与此图象有两个公共点时,
与此图象有两个公共点时,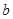 的取值范围.
的取值范围.