题目内容
(1)请先将下式化简,再选择一个你喜欢又使原式有意义的数代入求值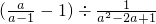 ;
;
(2)计算: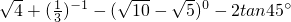 ;
;
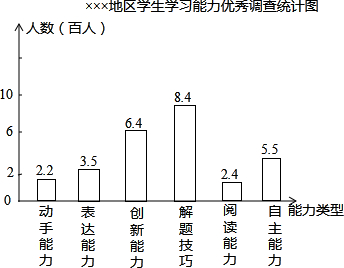
(3)某地为了解从2004年以来初中学生参加基础教育课程改革的情况,随机调查了本地区1000名初中学生学习能力优秀的情况.调查时,每名学生可以在动手能力,表达能力,创新能力,解题技巧,阅读能力和自主学习等六个方面中选择自己认为是优秀的项.调查后绘制了如图所示的统计图.请根据统计图反映的信息解答下列问题: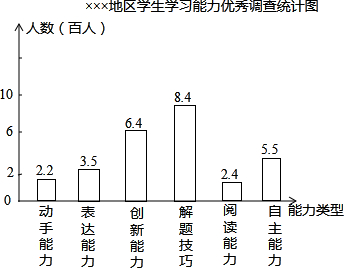
①学生获得优秀人数最多的一项和最有待加强的一项各是什么?
②这1000名学生平均每人获得几个项目为优秀?
③若该地区共有2万名初中学生,请估计他们表达能力为优秀的学生有多少人?
解:(1)原式=
=a-1;
(2)原式=2+3-1-2
=2;
(3)①人数最多的一项是:解题技巧,有840人;
有待加强的一项是:动手能力,有220人;
②根据图示,共有优秀项目(2.2+3.5+6.4+8.4+2.4+5.5)×100=2840项,这1000名学生平均每人获得 =2.84个项目为优秀;
=2.84个项目为优秀;
③请估计他们表达能力为优秀的学生有:20000×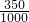 =7000人.
=7000人.
分析:(1)根据分式的计算法则;
(2)根据零指数幂,负整数指数知识点解答;
(3)将图中所示的信息转化为相关数据,再进行计算.
点评:在选择a的值时,易出现错误,比如选择a=1代入求值就是错误的运算,因为当a=1时,a-1虽然有意义,但是原分式无意义,故a的取值不能是1.

=a-1;
(2)原式=2+3-1-2
=2;
(3)①人数最多的一项是:解题技巧,有840人;
有待加强的一项是:动手能力,有220人;
②根据图示,共有优秀项目(2.2+3.5+6.4+8.4+2.4+5.5)×100=2840项,这1000名学生平均每人获得
 =2.84个项目为优秀;
=2.84个项目为优秀;③请估计他们表达能力为优秀的学生有:20000×
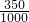 =7000人.
=7000人.分析:(1)根据分式的计算法则;
(2)根据零指数幂,负整数指数知识点解答;
(3)将图中所示的信息转化为相关数据,再进行计算.
点评:在选择a的值时,易出现错误,比如选择a=1代入求值就是错误的运算,因为当a=1时,a-1虽然有意义,但是原分式无意义,故a的取值不能是1.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目