题目内容
已知实系数一元二次方程ax2+2bx+c=0有两个实根x1、x2,且a>b>c,a+b+c=0,若则d=|x1-x2|的取值范围为 .
【答案】分析:根据根与系数的关系即可求得x1+x2=-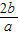 ,x1•x2=
,x1•x2=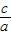 ,则可得d2=|x1-x2|2=(x1+x2)2-4x1•x2,又由a>b>c,a+b+c=0,得到函数f(
,则可得d2=|x1-x2|2=(x1+x2)2-4x1•x2,又由a>b>c,a+b+c=0,得到函数f(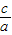 )=4[(
)=4[(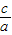 )2+
)2+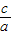 +1],根据其增减性即可求得答案.
+1],根据其增减性即可求得答案.
解答:解:∵实系数一元二次方程ax2+2bx+c=0有两个实根x1、x2,
∴x1+x2=-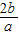 ,x1•x2=
,x1•x2=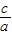 ,
,
∴d2=|x1-x2|2=(x1+x2)2-4x1•x2=(-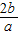 )2-
)2-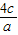 =
=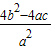 =
=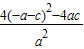 =4[(
=4[(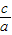 )2+
)2+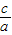 +1]=4[(
+1]=4[(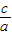 +
+ )2+
)2+ ]
]
∵a>b>c,a+b+c=0,
∴a>0,c<0,a>-a-c>c,
解得:-2<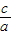 <-
<- ,
,
∵f(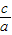 )=4[(
)=4[(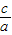 )2+
)2+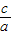 +1]的对称轴为:
+1]的对称轴为: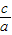 =-
=- ,
,
∴当-2<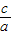 <-
<- 时,f(
时,f(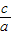 )=4[(
)=4[(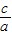 )2+
)2+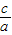 +1]是减函数,
+1]是减函数,
∴3<d2<12,
∴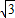 <d<2
<d<2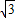 ,
,
即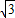 <|x1-x2|<2
<|x1-x2|<2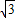 .
.
点评:此题主要考查了含有字母系数的一元二次方程的解法,注意根与系数的关系的应用.
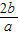 ,x1•x2=
,x1•x2=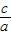 ,则可得d2=|x1-x2|2=(x1+x2)2-4x1•x2,又由a>b>c,a+b+c=0,得到函数f(
,则可得d2=|x1-x2|2=(x1+x2)2-4x1•x2,又由a>b>c,a+b+c=0,得到函数f(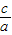 )=4[(
)=4[(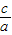 )2+
)2+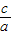 +1],根据其增减性即可求得答案.
+1],根据其增减性即可求得答案.解答:解:∵实系数一元二次方程ax2+2bx+c=0有两个实根x1、x2,
∴x1+x2=-
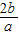 ,x1•x2=
,x1•x2=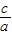 ,
,∴d2=|x1-x2|2=(x1+x2)2-4x1•x2=(-
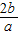 )2-
)2-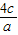 =
=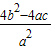 =
=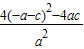 =4[(
=4[(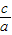 )2+
)2+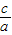 +1]=4[(
+1]=4[(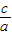 +
+ )2+
)2+ ]
]∵a>b>c,a+b+c=0,
∴a>0,c<0,a>-a-c>c,
解得:-2<
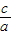 <-
<- ,
,∵f(
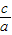 )=4[(
)=4[(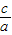 )2+
)2+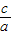 +1]的对称轴为:
+1]的对称轴为: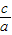 =-
=- ,
,∴当-2<
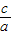 <-
<- 时,f(
时,f(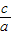 )=4[(
)=4[(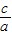 )2+
)2+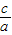 +1]是减函数,
+1]是减函数,∴3<d2<12,
∴
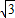 <d<2
<d<2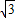 ,
,即
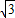 <|x1-x2|<2
<|x1-x2|<2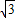 .
.点评:此题主要考查了含有字母系数的一元二次方程的解法,注意根与系数的关系的应用.

练习册系列答案
相关题目
 的一元二次方程
的一元二次方程 有实根,则
有实根,则 的取值范围是
的取值范围是 B.
B. C.
C.