题目内容
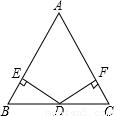
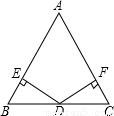
(A类)如图DE⊥AB,DF⊥AC,垂足分别为E,F,请你从下面三个条件中,再选出两个作为已知条件,另一个为结论,推出一个正确的命题(只需写出一种情况).

①AB=AC ②BD=CD③BE=CF
已知:DE⊥AB,DF⊥AC,垂足分别为E、F,________=________,________=________.
(B类)求证:
已知.…,AB=AC,BD=CD
求证:BE=CF
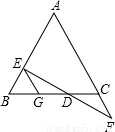
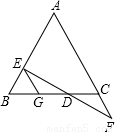
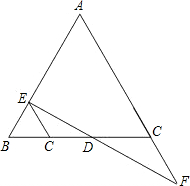
(A类)如图,EG∥AF,请你从下面三个条件中,再选两个作为已知条件,另一个为结论,推出一个正确的命题(只需写出一种情况).

①AB=AC②DE=DF③BE=CF
已知:EG∥AF,________=________,________=________
(B类)
已知…,AB=AC.DE=DF,求证:BE=CF.
AB AC BD DC AB AC DE DF
分析:(1)本题的条件是围绕三角形BED,DFC全等来展开的,已知了两组直角,要证全等,只要再知道一组对应角和一组对应边相等根据AAS,或ASA来求证,或知道斜边和直角边分别对应相等,根据斜边直角边定理来求证.
(2)根据题意本题是围绕三角形ECD,CDF来展开的.根据EG∥CF可以得出这两个三角形中的两组对应角相等,要证全等就必须知道一组对应边相等,即DE=DF,有了DE=DF,根据AAS便可得出两三角形全等的结论,于是EG=FC,如果已知AB=AC,那么根据等边对顶角可得出∠ABC=∠ACB,根据EG∥AF,同位角∠EGB=∠ACB,将相等的角进行置换后即可得出BE=GE,也就得出了BE=CF.
解答:证明:(1)∵AB=AC,
∴∠B=∠C.
∵∠DEB=∠CFD=90°,BD=DC,
∴△BED≌△CFD.
∴BE=CF.
(2)∵EG∥AF,
∴∠GEF=∠F,∠EGC=∠FCD.
∵DE=DF,
∴△GED≌△CFD.
∴EG=FC.
∵AB=AC,
∴∠B=∠ACB.
∵EG∥AF,
∴∠B=∠EGB=∠ACB.
∴BE=EG.
∴BE=FC.
点评:本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.
注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.
分析:(1)本题的条件是围绕三角形BED,DFC全等来展开的,已知了两组直角,要证全等,只要再知道一组对应角和一组对应边相等根据AAS,或ASA来求证,或知道斜边和直角边分别对应相等,根据斜边直角边定理来求证.
(2)根据题意本题是围绕三角形ECD,CDF来展开的.根据EG∥CF可以得出这两个三角形中的两组对应角相等,要证全等就必须知道一组对应边相等,即DE=DF,有了DE=DF,根据AAS便可得出两三角形全等的结论,于是EG=FC,如果已知AB=AC,那么根据等边对顶角可得出∠ABC=∠ACB,根据EG∥AF,同位角∠EGB=∠ACB,将相等的角进行置换后即可得出BE=GE,也就得出了BE=CF.
解答:证明:(1)∵AB=AC,
∴∠B=∠C.
∵∠DEB=∠CFD=90°,BD=DC,
∴△BED≌△CFD.
∴BE=CF.
(2)∵EG∥AF,
∴∠GEF=∠F,∠EGC=∠FCD.
∵DE=DF,
∴△GED≌△CFD.
∴EG=FC.
∵AB=AC,
∴∠B=∠ACB.
∵EG∥AF,
∴∠B=∠EGB=∠ACB.
∴BE=EG.
∴BE=FC.
点评:本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.
注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.

练习册系列答案
相关题目
 (A类)如图,DE⊥AB、DF⊥AC.垂足分别为E、F.请你从下面三个条件中,再选出两个作为已知条件,另一个为结论,推出一个正确的命题(只需写出一种情况).
(A类)如图,DE⊥AB、DF⊥AC.垂足分别为E、F.请你从下面三个条件中,再选出两个作为已知条件,另一个为结论,推出一个正确的命题(只需写出一种情况).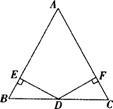 22、(A类)如图DE⊥AB,DF⊥AC,垂足分别为E,F,请你从下面三个条件中,再选出两个作为已知条件,另一个为结论,推出一个正确的命题(只需写出一种情况).
22、(A类)如图DE⊥AB,DF⊥AC,垂足分别为E,F,请你从下面三个条件中,再选出两个作为已知条件,另一个为结论,推出一个正确的命题(只需写出一种情况).