题目内容
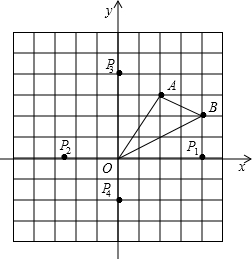
已知:点A、点B的坐标分别为(2,3)、(4,2),点O为平面直角坐标系的原点,点P在坐标轴上,若以A、B、O、P为顶点的四边形的面积等于△OAB的面积的2倍,则点P的坐标为分析:先利用“割补法”求出不规则△OAB的面积,只要“新增”三角形的面积等于△OAB的面积即可,在x轴、y轴上分别找出满足条件的P点.
解答:解:∵S△OAB=
×2×3+
×(2+3)×2-
×4×2=4,
要使以A、B、O、P为顶点的四边形的面积等于△OAB的面积的2倍,
只要“新增”三角形的面积为4即可;
∴当点P在x轴正半轴时,“新增”△OBP,则点P的坐标为(4,0)时,“新增”△OBP的面积为4,满足条件;
当点P在x轴负半轴时,“新增”△OAP,则点P的坐标为(-
,0)时,“新增”△OAP的面积为4,满足条件;
当点P在y轴正半轴时,“新增”△OAP,则点P的坐标为(0,4)时,“新增”△OAP的面积为4,但是A、B、O、P不能构成四边形,不满足条件;
当点P在y轴负半轴时,“新增”△OBP,则点P的坐标为(0,-2)时,“新增”△OBP的面积为4,满足条件;
故填:(4,0)、(-
,0)、(0,-2).
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
要使以A、B、O、P为顶点的四边形的面积等于△OAB的面积的2倍,
只要“新增”三角形的面积为4即可;
∴当点P在x轴正半轴时,“新增”△OBP,则点P的坐标为(4,0)时,“新增”△OBP的面积为4,满足条件;
当点P在x轴负半轴时,“新增”△OAP,则点P的坐标为(-
| 8 |
| 3 |
当点P在y轴正半轴时,“新增”△OAP,则点P的坐标为(0,4)时,“新增”△OAP的面积为4,但是A、B、O、P不能构成四边形,不满足条件;
当点P在y轴负半轴时,“新增”△OBP,则点P的坐标为(0,-2)时,“新增”△OBP的面积为4,满足条件;
故填:(4,0)、(-
| 8 |
| 3 |

点评:本题考查了平面直角坐标系中不规则三角形面积的求法“割补法”,同时考查了根据面积确定点的坐标的能力及分类讨论的思想.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

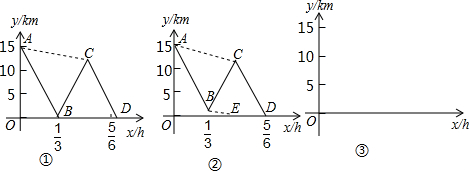
 h.图②中折线A-B-C-D、线段AC、线段BE分别表示王老师、甲、乙在上述过程中,离车站的路程y(km)与王老师所用时间x(h)之间的函数关系.求a的值.
h.图②中折线A-B-C-D、线段AC、线段BE分别表示王老师、甲、乙在上述过程中,离车站的路程y(km)与王老师所用时间x(h)之间的函数关系.求a的值.