题目内容
 如图所示,△ABC与△BDE都是等边三角形,AB<BD.若△ABC不动,将△BDE绕点B旋转,则在旋转过程中,AE与CD的大小关系为
如图所示,△ABC与△BDE都是等边三角形,AB<BD.若△ABC不动,将△BDE绕点B旋转,则在旋转过程中,AE与CD的大小关系为
- A.AE=CD
- B.AE>CD
- C.AE<CD
- D.无法确定
A
分析:本题可通过证△ABE和△CBD全等,来得出AE=CD的结论.两三角形中,已知了AB=BC、BE=BD,因此关键是证得∠ABE=∠CBD;由于△ABC和△BED都是等边三角形,因此∠EBD=∠ABC=60°,即∠ABE=∠CBD=120°,由此可得证.
解答:∵△ABC与△BDE都是等边三角形,
∴AB=BC,BE=BD,∠ABC=∠EBD=60°;
∴∠ABE=∠CBD=120°;
∴△ABE≌△CBD;
∴AE=CD.
故选A.
点评:本题考查了全等三角形的判定与性质,等边三角形的性质,当出现两个等边三角形时,一般要利用等边三角形的边和角从中找到一对全等三角形.
分析:本题可通过证△ABE和△CBD全等,来得出AE=CD的结论.两三角形中,已知了AB=BC、BE=BD,因此关键是证得∠ABE=∠CBD;由于△ABC和△BED都是等边三角形,因此∠EBD=∠ABC=60°,即∠ABE=∠CBD=120°,由此可得证.
解答:∵△ABC与△BDE都是等边三角形,
∴AB=BC,BE=BD,∠ABC=∠EBD=60°;
∴∠ABE=∠CBD=120°;
∴△ABE≌△CBD;
∴AE=CD.
故选A.
点评:本题考查了全等三角形的判定与性质,等边三角形的性质,当出现两个等边三角形时,一般要利用等边三角形的边和角从中找到一对全等三角形.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

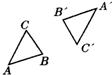 14、(一题多解)如图所示,△ABC与△A′B′C′关于点O中心对称,但点O不慎被涂掉了,请你帮排版工人找到对称中心O的位置.
14、(一题多解)如图所示,△ABC与△A′B′C′关于点O中心对称,但点O不慎被涂掉了,请你帮排版工人找到对称中心O的位置. 已知:如图所示,△ABC与△ABD中,∠C=∠D=90°,要使△ABC≌△ABD(HL)成立,还需要加的条件是( )
已知:如图所示,△ABC与△ABD中,∠C=∠D=90°,要使△ABC≌△ABD(HL)成立,还需要加的条件是( ) 如图所示,△ABC与△A′B′C′关于直线l成轴对称,已知∠ABC=80°,A′C′=
如图所示,△ABC与△A′B′C′关于直线l成轴对称,已知∠ABC=80°,A′C′=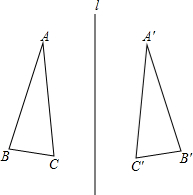 如图所示,△ABC与△A′B′C′关于直线ι成轴对称,已知∠B=80°,A′C′=10,那么∠B′=
如图所示,△ABC与△A′B′C′关于直线ι成轴对称,已知∠B=80°,A′C′=10,那么∠B′=