题目内容
【题目】如图，在等腰三角形
中，
，
为
边上中点，过点作
，交
于
，交
于
，若
，则的长为_________．
【答案】6
【解析】
连接BD，利用ASA证出△EDB≌△FDC，从而证出S△EDB=S△FDC，从而求出S△DBC，然后根据三角形的面积即可求出CD，从而求出AC，最后利用勾股定理即可求出结论．
解：连接BD
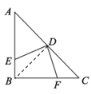
∵在等腰三角形
中，
，
为
边上中点，
∴AB=BC，BD=CD=AD，∠BDC=90°，∠EBD=
，∠C=45°
∵
∴∠EDF=∠BDC=90°，∠EBD=∠C=45°
∴∠EDB=∠FDC
在△EDB和△FDC中
∴△EDB≌△FDC
∴S△EDB=S△FDC
∴S△DBC= S△FDC＋S△BDF= S△EDB＋S△BDF=
∴
∴CD2=18
∴CD=
∴AC=2CD=
∴AB2＋BC2=AC2
∴2AB2=（）2
故答案为：6．
练习册系列答案
相关题目
