题目内容
如果两个角的两边分别平行,而其中一个角比另一个角的3倍少20°,那么这两个角的度数是
- A.50°和130°
- B.60°和120°
- C.65°和115°
- D.以上都不对
D
分析:首先由两个角的两边分别平行,可得这两个角相等或互补.然后设其中一角为x°,由其中一个角比另一个角的3倍少20°,然后分别从两个角相等与互补去分析,即可求得答案,注意别漏解.
解答:∵两个角的两边分别平行,
∴这两个角相等或互补.
设其中一角为x°,
若这两个角相等,则x=3x-20,
解得:x=10,
∴这两个角的度数是10°和10°;
若这两个角互补,
则180-x=3x-20,
解得:x=50,
∴这两个角的度数是50°和130°.
∴这两个角的度数是10°和10°或50°和130°.
故选D.
点评:此题考查了平行线的性质与一元一次方程的解法.此题难度适中,解题的关键是掌握如果两个角的两边分别平行,则这两个角相等或互补,注意方程思想的应用.
分析:首先由两个角的两边分别平行,可得这两个角相等或互补.然后设其中一角为x°,由其中一个角比另一个角的3倍少20°,然后分别从两个角相等与互补去分析,即可求得答案,注意别漏解.
解答:∵两个角的两边分别平行,
∴这两个角相等或互补.
设其中一角为x°,
若这两个角相等,则x=3x-20,
解得:x=10,
∴这两个角的度数是10°和10°;
若这两个角互补,
则180-x=3x-20,
解得:x=50,
∴这两个角的度数是50°和130°.
∴这两个角的度数是10°和10°或50°和130°.
故选D.
点评:此题考查了平行线的性质与一元一次方程的解法.此题难度适中,解题的关键是掌握如果两个角的两边分别平行,则这两个角相等或互补,注意方程思想的应用.

练习册系列答案
相关题目
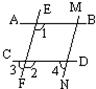 22、如图:
22、如图: 33、如图,AB∥CD,EF∥MN,∠1=115°.
33、如图,AB∥CD,EF∥MN,∠1=115°.