题目内容
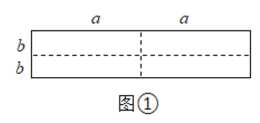
【题目】如图①是一个长为![]() ,宽为
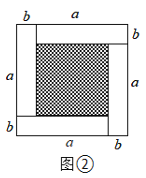
,宽为![]() 的长方形,沿图中的虚线剪开均分成四个小长方形,然后按图②形状拼成一个正方形.
的长方形,沿图中的虚线剪开均分成四个小长方形,然后按图②形状拼成一个正方形.
(1)若![]() ,
,![]() .求图②中阴影部分面积;
.求图②中阴影部分面积;
(2)观察图②,写出![]() ,
,![]() ,
,![]() 三个代数式之间的等量关系.(简要写出推理过程)
三个代数式之间的等量关系.(简要写出推理过程)
(3)根据(2)题的等量关系,完成下列问题:若![]() ,
,![]() ,求
,求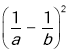 的值.
的值.
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() ,过程见解析;(3)
,过程见解析;(3)![]()
【解析】
(1)根据图形可知,阴影正方形的边长为小长方形的长与宽的差,写出即可求解;
(2)根据完全平方公式的变形即可得到关系式;
(3)根据![]() ,故求出
,故求出 ,代入(2)中的公式即可求解.
,代入(2)中的公式即可求解.
解:(1)∵阴影正方形的边长为小长方形的长与宽的差,
即阴影正方形的边长为13-3=10
∴![]() ;
;
(2)结论:![]() 或
或![]()
∵ ![]() ,
,![]()
∴![]()
∴![]() 或
或![]() ;
;
(3) ∵![]() ,
,![]()
∴![]()
∴
由(2)可知![]()
∴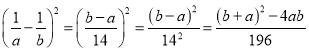
∵![]() ,
,![]()
∴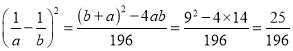 .
.

练习册系列答案
相关题目