题目内容
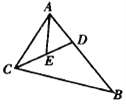
【题目】如图，在△ABC中，∠BAC=60°，BC=18，D是AB上一点，AC=BD，E是CD的中点.则AE的长是( ).
A. 12 B. 9 C. 9
D. 以上都不对
【答案】B
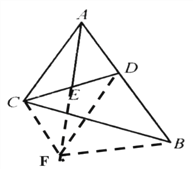
【解析】试题分析：如图所示，过D作DF∥AC，交AE的延长线于F，连接BF，CF，由此可得△DEF≌△CEA，根据全等三角形的性质可得AE=EF，因此可根据对角线互相平分的四边形是平行四边形，可得四边形ACFD是平行四边形，可得AC=DF，∠FDB=∠BAC=60°，∠ACF=120°，然后根据AC=BD，可得△DBF是等边三角形，可得AC=DF=DB=FB,∠BFC=120°，所以△ACF≌△BFC，因此可知BC=AF=2AE=18，解得AE=9.
故选：B
练习册系列答案
相关题目
