题目内容
【题目】（1）如图1，已知射线OA，OB，OC，OD，∠AOD＝∠BOC＝α．
①若α＝38°，∠COD＝30°，求∠BOD、∠AOC的度数；
②若∠COD＝25°，请找出图中与∠BOD相等的角，并通过计算说明理由；
（2）如图2，∠MPN是钝角，请利用三角尺画特殊角的功能，在图2中画一个与∠MPN相等的角．（标出图中特殊角的度数，并写出与∠MPN相等的角）
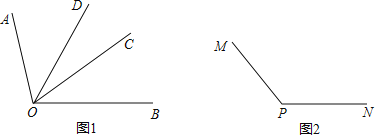
【答案】（1）①68°，68°，②∠AOC＝∠BOD，见解析；（2）见解析
【解析】
（1）①依据∠AOD＝∠BOC＝α＝38°，∠COD＝30°，即可得到∠BOD＝38°+30°＝68°，∠AOC＝38°+30°＝68°；②依据∠AOD＝∠BOC＝α，∠COD＝25°，即可得到∠AOD+∠COD＝∠BOC+∠COD＝α+25°，进而得出∠AOC＝∠BOD；
（2）依据直角三角板作∠NPE＝90°，∠MPF＝90°，依据等式的性质即可得到∠EPF＝∠MPN．
解：（1）①∵∠AOD＝∠BOC＝α＝38°，∠COD＝30°，
∴∠BOD＝38°+30°＝68°，∠AOC＝38°+30°＝68°；
②∠BOD与∠BOD相等．
∵∠AOD＝∠BOC＝α，∠COD＝25°，
∴∠AOD+∠COD＝∠BOC+∠COD＝α+25°，
∴∠AOC＝∠BOD；
（2）如图所示，∠EPF即为所求．
【题目】近来，校园安全问题引起了社会的极大关注．为了了解学生对安全知识的掌握情况，某校随机抽取了40名学生进行安全知识测试，测试成绩（百分制）如下：
78 86 74 81 75 76 87 70 75 90
75 79 81 70 74 80 86 69 83 77
93 73 88 81 72 81 94 83 77 83
80 81 70 81 73 78 82 80 70 50
（1）本次测试属于 （填“普查”或“抽样调查”）；
（2）若按如下分数段整理成绩，则表中的a＝ ，b＝ ；
成绩x | 50≤x＜60 | 60≤x＜70 | 70≤x＜80 | 80≤x＜90 | 90≤x＜100 |
人数 | 1 | a | 18 | b | 3 |
（3）若用（2）中数据制作扇形统计图，求表示“70≤x＜80”的扇形的圆心角度数；
（4）已知该校共有2000名学生，若规定成绩80分及以上为优秀，估计该校学生对安全知识掌握情况是优秀的有多少人？
