题目内容
观察下列各个等式:12=1,12+22=5,12+22+32=14,12+22+32+42=30,….(1)你能从中推导出计算12+22+32+42+…+n2的公式吗?请写出你的推导过程;
(2)请你用(1)中推导出的公式来解决下列问题:
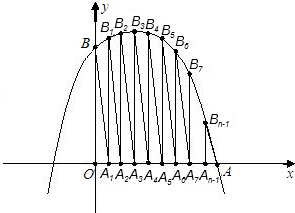
已知:如图,抛物线y=-x2+2x+3与x、y轴的正半轴分别交于点A、B,将线段OAn等分,分点从左到右依次为A1、A2、A3、A4、A5、A6、…、An-1,分别过这n-1个点作x轴的垂线依次交抛物线于点B1、B2、B3、B4、B5、B6、…、Bn-1,设△OBA1、
△A1B1A2、△A2B2A3、△A3B3A4、…、△An-1Bn-1A的面积依次为S1、S2、S3、S4、…、Sn.
①当n=2010时,求S1+S2+S3+S4+S5+…+S2010的值;
②试探究:当n取到无穷无尽时,题中所有三角形的面积和将是什么值?为什么?

【答案】分析:(1)由n3-(n-1)3=3n2-3n+1公式的n的式子相加推导出12+22+32+42+…+n2的公式.
(2)①结合抛物线和(1)中推导出的公式求出S1+S2+S3+S4+S5+…+S2010的值;
②当n取到无穷无尽时,取极值,求得三角形的面积.
解答:解:(1)∵n3-(n-1)3=3n2-3n+1,∴当式中的n从1、2、3、依次取到n时,就可得下列n个等式:
13-03=3-3+1,23-13=3×22-3×2+1,33-23=3×32-3×3+1,…,n3-(n-1)3=3n2-3n+1,
将这n个等式的左右两边分别相加得:n3=3×(12+22+32+…+n2)-3×(1+2+3+…+n)+n,
即12+22+32+42+…+n2= .
.
(2)先求得A、B两点的坐标分别为(3,0)、(0,3),
∴点A1、A2、A3、A4、A5、A6、…、An-1的横坐标分别为 ,
,
点B1、B2、B3、B4、B5、B6、…、Bn-1的纵坐标分别为 .
.
∴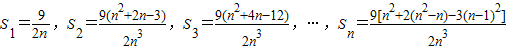 ;
;
∴ =
= .(3分)
.(3分)
∴①当n=2010时,S1+S2+S3+S4+S5+…+S2010= +
+ -
- ;
;
②∵ ;
;
∴当n取到无穷无尽时,上式的值等于 ,即所有三角形的面积和等于
,即所有三角形的面积和等于 .(3分)
.(3分)
点评:本题通过推导公式考查了二次函数图象上点的坐标特征,题目新颖,有一定的难度.
(2)①结合抛物线和(1)中推导出的公式求出S1+S2+S3+S4+S5+…+S2010的值;
②当n取到无穷无尽时,取极值,求得三角形的面积.
解答:解:(1)∵n3-(n-1)3=3n2-3n+1,∴当式中的n从1、2、3、依次取到n时,就可得下列n个等式:
13-03=3-3+1,23-13=3×22-3×2+1,33-23=3×32-3×3+1,…,n3-(n-1)3=3n2-3n+1,
将这n个等式的左右两边分别相加得:n3=3×(12+22+32+…+n2)-3×(1+2+3+…+n)+n,
即12+22+32+42+…+n2=
 .
.(2)先求得A、B两点的坐标分别为(3,0)、(0,3),
∴点A1、A2、A3、A4、A5、A6、…、An-1的横坐标分别为
 ,
,点B1、B2、B3、B4、B5、B6、…、Bn-1的纵坐标分别为
 .
.∴
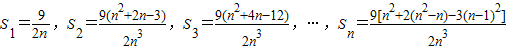 ;
;∴
 =
= .(3分)
.(3分)∴①当n=2010时,S1+S2+S3+S4+S5+…+S2010=
 +
+ -
- ;
;②∵
 ;
;∴当n取到无穷无尽时,上式的值等于
 ,即所有三角形的面积和等于
,即所有三角形的面积和等于 .(3分)
.(3分)点评:本题通过推导公式考查了二次函数图象上点的坐标特征,题目新颖,有一定的难度.

练习册系列答案
相关题目
 S2、S3、S4、…、Sn.
S2、S3、S4、…、Sn. S2、S3、S4、…、Sn.
S2、S3、S4、…、Sn.