题目内容
【题目】已知抛物线![]() .
.
![]() 求出抛物线的对称轴方程以及与
求出抛物线的对称轴方程以及与![]() 轴的交点坐标
轴的交点坐标
![]() 当
当![]() 时,求出抛物线与
时,求出抛物线与![]() 轴的交点坐标
轴的交点坐标
![]() 已知
已知![]() 三点构成三角形
三点构成三角形![]() ,当抛物线与三角形
,当抛物线与三角形![]() 的三条边一共有
的三条边一共有![]() 个交点时,直接写出
个交点时,直接写出![]() 的取值范围.
的取值范围.
【答案】(1)x=2,(0,3);(2)(![]() ,0),(
,0),(![]() ,0);(3):0<m<
,0);(3):0<m<![]() 或m>1
或m>1
【解析】
(1)根据抛物线对称轴为![]() 求得对称轴方程,令x=0,可得与y轴的交点坐标;
求得对称轴方程,令x=0,可得与y轴的交点坐标;
(2)令m=2,y=0,解方程即可得出与x轴的交点坐标;
(3)分别将抛物线经过点A、与x轴只有一个交点时的图像画出,结合图像讨论m的取值范围.
解:(1)∵![]() ,
,
∴对称轴的方程为![]() ,
,
令x=0,y=3,
∴与y轴交点坐标为(0,3);
(2)∵m=2,令y=0,
则![]() ,
,
解得![]() ,
,![]() ,
,
∴抛物线与x轴交点坐标为(![]() ,0),(
,0),(![]() ,0);
,0);
(3)由题意可得:![]() ,
,
可得抛物线经过点(0,3),(4,3),不经过点B,
抛物线对称轴为直线x=2,A(1,0),B(4,0),
如图1,当抛物线开口无限小时,即m无限大,抛物线与△ABC有两个交点;
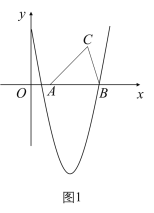
如图2,当抛物线经过点A时,抛物线与△ABC恰好有3个交点,
此时,将点A(1,0)代入,
解得:m=1;
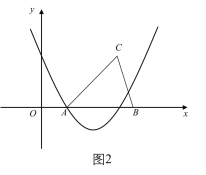
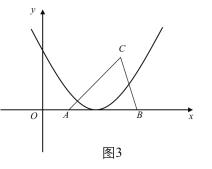
如图3,当抛物线与x轴只有1个交点时,抛物线与△ABC恰好有3个交点,
此时,![]() ,
,
解得:m=![]() 或0(舍);
或0(舍);
综上:若抛物线与△ABC的三条边一共有![]() 个交点时,
个交点时,
m的取值范围是:0<m<![]() 或m>1.
或m>1.

 导学全程练创优训练系列答案
导学全程练创优训练系列答案【题目】如图1,A,B,C是郑州市二七区三个垃圾存放点,点B,C分别位于点A的正北和正东方向,AC=40米.八位环卫工人分别测得的BC长度如下表:
甲 | 乙 | 丙 | 丁 | 戊 | 戌 | 申 | 辰 | |
BC(单位:米) | 84 | 76 | 78 | 82 | 70 | 84 | 86 | 80 |
他们又调查了各点的垃圾量,并绘制了下列尚不完整的统计图2,图3:
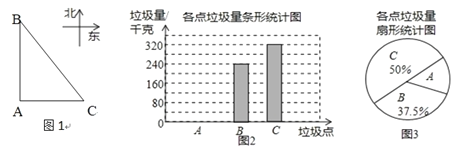
(1)表中的中位数是 、众数是 ;
(2)求表中BC长度的平均数![]() ;
;
(3)求A处的垃圾量,并将图2补充完整;
(4)用(2)中的![]() 作为BC的长度,要将A处的垃圾沿道路AB都运到B处,已知运送1千克垃圾每米的费用为0.005元,求运垃圾所需的费用.
作为BC的长度,要将A处的垃圾沿道路AB都运到B处,已知运送1千克垃圾每米的费用为0.005元,求运垃圾所需的费用.
【题目】某校初一年级68名师生参加社会实践活动,计划租车前往,租车收费标准如下:
车型 | 大巴车 (最多可坐55人) | 中巴车 (最多可坐39人) | 小巴车 (最多可坐26人) |
每车租金 (元∕天) | 900 | 800 | 550 |
则租车一天的最低费用为____元.