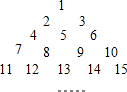
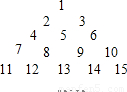题目内容
 观察下列三角形数阵:则第50行的最后一个数是( )
观察下列三角形数阵:则第50行的最后一个数是( )| A、1225 | B、1260 | C、1270 | D、1275 |
分析:第一行的最后一个数是1,第二行的最后一个数是1+2=3,第三行的最后一个数是1+2+3=6,…依此类推,第n行的最后一个数是1+2+3+…+n=
.
当n=50时,原式=1275.
| n(n+1) |
| 2 |
当n=50时,原式=1275.
解答:解:求的第50行的最后一个数是:
三角形数阵中1,3,6,10,15,…这列数的第50个数.
1,3,6,10,15,…中,
1=
×1×(1+1)
3=
×2×(2+1)
6=
×3×(3+1)
10=
×4×(4+1)
15=
×5×(5+1)
…
由此可得到第n个数表示为:
n(n+1).
因此第50个数为:
×50×(50+1)=1275.
即即第50行的最后一个数是1275.
故选D.
三角形数阵中1,3,6,10,15,…这列数的第50个数.
1,3,6,10,15,…中,
1=
| 1 |
| 2 |
3=
| 1 |
| 2 |
6=
| 1 |
| 2 |
10=
| 1 |
| 2 |
15=
| 1 |
| 2 |
…
由此可得到第n个数表示为:
| 1 |
| 2 |
因此第50个数为:
| 1 |
| 2 |
即即第50行的最后一个数是1275.
故选D.
点评:本题是一道找规律的题目,要求学生通过观察,分析、归纳发现其中的规律,并应用发现的规律解决问题.此题重点看各行的最后一个数的规律.

练习册系列答案
相关题目
观察下列三角形数阵:
则第50行的最后一个数是( )
| 1 | ||||||||
| 2 | 3 | |||||||
| 4 | 5 | 6 | ||||||
| 7 | 8 | 9 | 10 | |||||
| 11 | 12 | 13 | 14 | 15 | ||||
| … | … |
| A、1225 | B、1260 |
| C、1270 | D、1275 |