题目内容
4、点P到△ABC三边的距离相等，则点P是△ABC的什么交点（ ）
分析：由角平分线性质的逆定理可得，点P是△ABC的角平分线的交点．
解答：解：∵点P到△ABC三边的距离相等，
∴点P是△ABC的角平分线的交点（角平分线性质的逆定理）．
故选C．
∴点P是△ABC的角平分线的交点（角平分线性质的逆定理）．
故选C．
点评：此题主要考查角平分线的性质的逆定理：到角的两边的距离相等的点在角的平分线上．
练习册系列答案
口算心算速算应用题系列答案
同步拓展阅读系列答案
相关题目
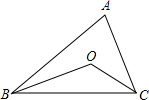△ABC中，点O是△ABC内一点，且点O到△ABC三边的距离相等；∠A=40°，则∠BOC=（ ）| A、110° | B、120° | C、130° | D、140° |
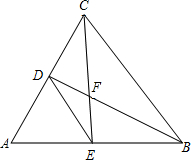如图，在△ABC中，∠A=60°，∠ABC，∠ACB的平分线分别交AC、AB于点D，E，CE、BD相交于点F，连接DE．下列结论：①cos∠BFE=
| 1 |
| 2 |
| 1 |
| 2 |
④点F到△ABC三边的距离相等；⑤BE+CD=BC．
其中正确的结论是（ ）
| A、②③④ | B、②④⑤ |
| C、①④⑤ | D、①③④ |
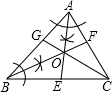如图，根据尺规作图的痕迹，判断下列说法不正确的是（ ）| A、AE、BF是△ABC的内角平分线 | B、CG也是△ABC的一条内角平分线 | C、点O到△ABC三边的距离相等 | D、AO=BO=CO |