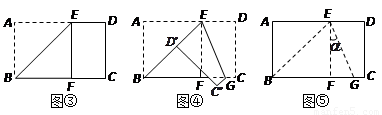题目内容
 如图,?ABCD在平面直角坐标系中,AD=6,若OA、OB的长是关于x的一元二次方程x2-7x+12=0的两个根,且OA>OB.
如图,?ABCD在平面直角坐标系中,AD=6,若OA、OB的长是关于x的一元二次方程x2-7x+12=0的两个根,且OA>OB.
(1)求直线CD的解析式;
(2)是否存在x轴上的点E,使得以A、O、E为顶点的三角形与△DAO相似?若存在,请写出符合条件的点E的坐标;若不存在,请说明理由.
解:(1)∵x2-7x+12=0,
∴(x-3)(x-4)=0,
解得:x=3或x=4,
∵OA、OB的长是关于x的一元二次方程x2-7x+12=0的两个根,且OA>OB,
∴OA=4,OB=3,
∴点A(0,4),点B(-3,0),
∵四边形ABCD是平行四边形,
∴BC=AD=6,
∴OC=BC-OB=3,
∴点C(3,0),点D(6,4),
设直线CD的解析式为:y=kx+b,
∴ ,
,
解得: ,
,
故直线CD的解析式为:y= x-4;
x-4;

(2)存在.
∵点E在x轴上,
∴∠AOE=90°,
∵△DAO中,∠DAO=90°,
∴∠AOE=∠DAO,
当OA:AD=OE:OA时,△OAE∽△ADO,
∴ ,
,
解得:OE= ,
,
∴点E的坐标为:( ,0)或(-
,0)或(- ,0);
,0);
当OA:OA=OE:AD时,△OAE∽△AOD,
∴ ,
,
解得:OE=6,
∴点E的坐标为:(6,0)或(-6,0);
∴符合条件的点E的坐标为:( ,0),(-
,0),(- ,0),(6,0)或(-6,0).
,0),(6,0)或(-6,0).
分析:(1)由OA、OB的长是关于x的一元二次方程x2-7x+12=0的两个根,且OA>OB,即可求得OA与OB的长,又由?ABCD在平面直角坐标系中,AD=6,可求得点D的坐标,继而求得点C的坐标,然后利用待定系数法求得直线CD的解析式;
(2)由在x轴上的点E,使得以A、O、E为顶点的三角形与△DAO相似,可得∠AOE=∠OAD=90°,然后由相似三角形的性质,即可求得符合条件的点E的坐标.
点评:此题考查了平行四边形的性质、一元二次方程的解法、待定系数法求一次函数的解析式以及相似三角形的判定与性质.此题难度适中,注意掌握方程思想、分类讨论思想与数形结合思想的应用.
∴(x-3)(x-4)=0,
解得:x=3或x=4,
∵OA、OB的长是关于x的一元二次方程x2-7x+12=0的两个根,且OA>OB,
∴OA=4,OB=3,
∴点A(0,4),点B(-3,0),
∵四边形ABCD是平行四边形,
∴BC=AD=6,
∴OC=BC-OB=3,
∴点C(3,0),点D(6,4),
设直线CD的解析式为:y=kx+b,
∴
 ,
,解得:
 ,
,故直线CD的解析式为:y=
 x-4;
x-4;
(2)存在.
∵点E在x轴上,
∴∠AOE=90°,
∵△DAO中,∠DAO=90°,
∴∠AOE=∠DAO,
当OA:AD=OE:OA时,△OAE∽△ADO,
∴
 ,
,解得:OE=
 ,
,∴点E的坐标为:(
 ,0)或(-
,0)或(- ,0);
,0);当OA:OA=OE:AD时,△OAE∽△AOD,
∴
 ,
,解得:OE=6,
∴点E的坐标为:(6,0)或(-6,0);
∴符合条件的点E的坐标为:(
 ,0),(-
,0),(- ,0),(6,0)或(-6,0).
,0),(6,0)或(-6,0).分析:(1)由OA、OB的长是关于x的一元二次方程x2-7x+12=0的两个根,且OA>OB,即可求得OA与OB的长,又由?ABCD在平面直角坐标系中,AD=6,可求得点D的坐标,继而求得点C的坐标,然后利用待定系数法求得直线CD的解析式;
(2)由在x轴上的点E,使得以A、O、E为顶点的三角形与△DAO相似,可得∠AOE=∠OAD=90°,然后由相似三角形的性质,即可求得符合条件的点E的坐标.
点评:此题考查了平行四边形的性质、一元二次方程的解法、待定系数法求一次函数的解析式以及相似三角形的判定与性质.此题难度适中,注意掌握方程思想、分类讨论思想与数形结合思想的应用.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案
相关题目




 处,折痕为EG(如图④);再展平纸片(如图⑤).试问:图⑤中∠
处,折痕为EG(如图④);再展平纸片(如图⑤).试问:图⑤中∠ 的大小是多少?(直接回答,不用说明理由).
的大小是多少?(直接回答,不用说明理由).