题目内容
 如图⊙O的半径为2,C1是函数y=
如图⊙O的半径为2,C1是函数y=| 1 |
| 2 |
| 1 |
| 2 |
分析:根据二次函数的性质可知C1与C2的图象关于x轴对称,从而得到x轴下方阴影部分的面积正好等于x轴上方空白部分的面积,所以,阴影部分的面积等于⊙O的面积的一半,然后列式计算即可得解.
解答:解:∵
与-
互为相反数,
∴C1与C2的图象关于x轴对称,
∴x轴下方阴影部分的面积正好等于x轴上方空白部分的面积,
∴阴影部分的面积=
×π•22=2π.
故选B.
| 1 |
| 2 |
| 1 |
| 2 |
∴C1与C2的图象关于x轴对称,
∴x轴下方阴影部分的面积正好等于x轴上方空白部分的面积,
∴阴影部分的面积=
| 1 |
| 2 |
故选B.
点评:本题考查了二次函数的图象,根据函数的对称性判断出阴影部分的面积等于⊙O的面积的一半是解题的关键,也是本题的难点.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
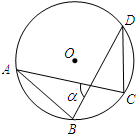 如图⊙O的半径为1,弦AB,CD的长度分别为
如图⊙O的半径为1,弦AB,CD的长度分别为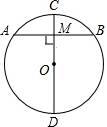 已知:如图⊙O的半径为5,CD为直径,AB为弦,CD⊥AB于M,若AB=6,求DM的长.
已知:如图⊙O的半径为5,CD为直径,AB为弦,CD⊥AB于M,若AB=6,求DM的长.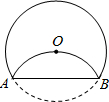 如图圆的半径为10,将圆的劣弧AB沿弦AB翻折后所得圆弧恰好经过圆心O,则折痕AB的长为( )
如图圆的半径为10,将圆的劣弧AB沿弦AB翻折后所得圆弧恰好经过圆心O,则折痕AB的长为( ) 已知如图⊙O的半径为3,过⊙O外的一点B作⊙O的切线BM,M为切点,BO交⊙O于A,过A点作BO的垂线,交BM于P点,BO=5,求:MP的长.
已知如图⊙O的半径为3,过⊙O外的一点B作⊙O的切线BM,M为切点,BO交⊙O于A,过A点作BO的垂线,交BM于P点,BO=5,求:MP的长.