题目内容
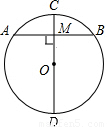
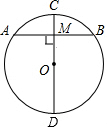已知：如图⊙O的半径为5，CD为直径，AB为弦，CD⊥AB于M，若AB=6，求DM的长．分析：连接OA，根据垂径定理可知AM的长，根据勾股定理可将OM的长求出，从而可将DM的长求出．
解答：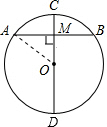
解：连接OA，
∵CD为直径，AB为弦，AB⊥CD，AB=6，
∴根据垂径定理可知AM=
AB=3，
在Rt△OAM中，OA=5，OM=
=4，
∴DM=OD+OM=9．
解：连接OA，∵CD为直径，AB为弦，AB⊥CD，AB=6，
∴根据垂径定理可知AM=
| 1 |
| 2 |
在Rt△OAM中，OA=5，OM=
| OA2-AM2 |
∴DM=OD+OM=9．
点评：本题综合考查了垂径定理和勾股定理的求法及性质．
练习册系列答案
小题狂做系列答案
相关题目
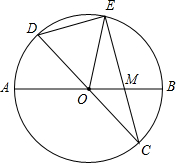已知：如图，在半径为4的⊙O中，AB、CD是两条直径，M为OB的中点，CM的延长线交⊙O于点E，且EM＞MC．连接DE，DE=
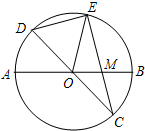已知：如图，在半径为8的⊙O中，AB，CD是两条直径，M为OB的中点，CM的延长线交⊙O于点E，且EM＞MC．连接DE，DE=
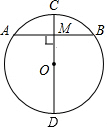已知：如图⊙O的半径为5，CD为直径，AB为弦，CD⊥AB于M，若AB=6，求DM的长．