题目内容
【题目】在平面直角坐标系中，对于点P（m，n）和点Q（x，y）．给出如下定义：若
，则称点Q为点P的“伴随点”．例如：点（1，2）的“伴随点”为点（5，0）．
（1）若点Q（﹣2，﹣4）是一次函数y＝kx+2图象上点P的“伴随点”，求k的值．
（2）已知点P（m，n）在抛物线C1：y＝
上，设点P的“伴随点”Q（x，y）的运动轨迹为C2．
①直接写出C2对应的函数关系式．
②抛物线C1的顶点为A，与x轴的交点为B（非原点），试判断在x轴上是否存在点M，使得以A、B、Q、M为顶点的四边形是平行四边形？若存在，求点M的坐标；若不存在，说明理由．
③若点P的横坐标满足﹣2≤m≤a时，点Q的纵坐标y满足﹣3≤y≤1，直接写出a的取值范围．
【答案】(1)
;(2) ①y＝
x2﹣3x+6;②见解析;③2≤a≤6.
【解析】
（1）根据伴随点定义可求k的值
（2）①根据伴随点的定义可求C2的解析式
②先求A，B坐标，以A、B、Q、M为顶点的四边形是平行四边形，则分三类讨论，根据平行四边形的性质可求M点坐标
③由x＝m+4可得 2≤x≤a+4，且抛物线顶点坐标为（6，﹣3），﹣3≤y≤1可得6≤a+4≤10，可求a的取值范围．
解（1）设P（x，kx+2）
根据题意得：
解得：
（2）①根据题意可得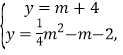
∴
∴C2的解析式：，
②∵抛物线C1：
∴B（4，0），A（2，﹣1）
∵以A、B、Q、M为顶点的四边形是平行四边形
∴若BA为边，BM为边，则AB∥MQ，AQ∥BM
∴Q与A的纵坐标相同
∴
∴
解得：
∴
或
，
∵AQ＝BM，A（4，0）
∴
或
，
若AB为边，BM为对角线，
∴对角线AQ与BM互相平分且交点在x轴上
∴Q点纵坐标为1
∴
解得x1＝2，x2＝10
∴AQ中点横坐标为6或2，且AQ与BM互相平分
∴M（8，0）或（0，0）
若BM为边，AB为对角线，
∴AB的中点
且AB与MQ互相平分
∴Q
或
∵MQ的中点为，
∴M
或
，
∴综上所述M或，（0，0），（ 8，0）
，.
③∵x＝m+4，﹣2≤m≤a
∴2≤x≤4+a
∵C2的解析式：
∴顶点坐标为（6，﹣3）
∵﹣3≤y≤1
∴当y＝1时，x＝2或10
∴6≤4+a≤10
∴2≤a≤6.
