题目内容
 宽与长之比为
宽与长之比为
| ||
| 2 |
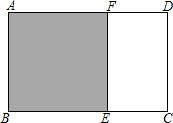
分析:判断黄金矩形的依据是:宽与长之比为
:1,判断出矩形DFEC的宽与长的比是不是
:1,利用AB=DC=AF和
=
,通过等量代换,求得
=
,得到矩形CDFE是黄金矩形.
| ||
| 2 |
| ||
| 2 |
| AB |
| AD |
| ||
| 2 |
| FD |
| DC |
| ||
| 2 |
解答:解:留下的矩形CDFE是黄金矩形.
证明:∵四边形ABEF是正方形,
∴AB=DC=AF,
又∵
=
,
∴
=
,
即点F是线段AD的黄金分割点,
∴
=
=
,
即
=
,
∴矩形CDFE是黄金矩形.
证明:∵四边形ABEF是正方形,
∴AB=DC=AF,
又∵
| AB |
| AD |
| ||
| 2 |
∴
| AF |
| AD |
| ||
| 2 |
即点F是线段AD的黄金分割点,
∴
| FD |
| AF |
| AF |
| AD |
| ||
| 2 |
即
| FD |
| DC |
| ||
| 2 |
∴矩形CDFE是黄金矩形.
点评:要求熟练掌握多边形相似的比例关系.会利用相似比,求未知线段的长度或比值.如上题中的矩形ABCD与矩形DFEC相似.

练习册系列答案
相关题目
