题目内容
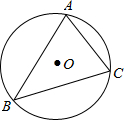 已知△ABC的外接圆O的半径为3,AC=4,则sinB=
已知△ABC的外接圆O的半径为3,AC=4,则sinB=
- A.

- B.

- C.

- D.

D
分析:作辅助线(连接AO并延长交圆于E,连CE) 构造直角三角形ACE,在直角三角形中根据锐角三角函数的定义求得角E的正弦值;然后由同弧所对的圆周角相等知∠B=∠E;最后由等量代换求得∠B的正弦值,并作出选择.
解答: 解:连接AO并延长交圆于E,连CE.
解:连接AO并延长交圆于E,连CE.
∴∠ACE=90°(直径所对的圆周角是直角);
在直角三角形ACE中,AC=4,AE=6,
∴sin∠E= =
= ;
;
又∵∠B=∠E(同弧所对的圆周角相等),
∴sinB= .
.
故选D.
点评:本题主要考查了圆周角定理、锐角三角函数的定义.在求锐角三角函数值时,一般是通过作辅助线构造直角三角形,在直角三角形中解三角函数的三角函数值即可.
分析:作辅助线(连接AO并延长交圆于E,连CE) 构造直角三角形ACE,在直角三角形中根据锐角三角函数的定义求得角E的正弦值;然后由同弧所对的圆周角相等知∠B=∠E;最后由等量代换求得∠B的正弦值,并作出选择.
解答:
 解:连接AO并延长交圆于E,连CE.
解:连接AO并延长交圆于E,连CE.∴∠ACE=90°(直径所对的圆周角是直角);
在直角三角形ACE中,AC=4,AE=6,
∴sin∠E=
 =
= ;
;又∵∠B=∠E(同弧所对的圆周角相等),
∴sinB=
 .
.故选D.
点评:本题主要考查了圆周角定理、锐角三角函数的定义.在求锐角三角函数值时,一般是通过作辅助线构造直角三角形,在直角三角形中解三角函数的三角函数值即可.

练习册系列答案
相关题目
 如图,已知△ABC的外接圆⊙O的半径为1,D,E分别为AB,AC的中点,则sin∠BAC的值等于线段( )
如图,已知△ABC的外接圆⊙O的半径为1,D,E分别为AB,AC的中点,则sin∠BAC的值等于线段( )| A、BC的长 | B、DE的长 | C、AD的长 | D、AE的长 |
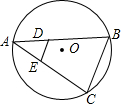 如图,已知△ABC的外接圆⊙O的半径为1,D、E分别是AB、AC上的点,BD=2AD,EC=2AE,则sin∠BAC的值等于线段( )
如图,已知△ABC的外接圆⊙O的半径为1,D、E分别是AB、AC上的点,BD=2AD,EC=2AE,则sin∠BAC的值等于线段( )| A、DE的长 | ||
| B、BC的长 | ||
C、
| ||
D、
|
 已知△ABC的外接圆O的半径为3,AC=4,则sinB=( )
已知△ABC的外接圆O的半径为3,AC=4,则sinB=( )A、
| ||
B、
| ||
C、
| ||
D、
|
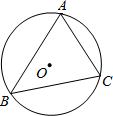 (2012•河东区一模)如图,已知△ABC的外接圆O的半径为
(2012•河东区一模)如图,已知△ABC的外接圆O的半径为 作图题(不写作法,保留作图痕迹)
作图题(不写作法,保留作图痕迹)