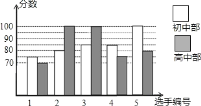
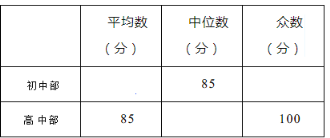
题目内容
【题目】探索规律:将连续的偶数2,4,6,8,…,排列如下表:
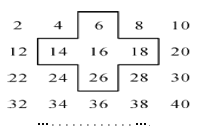
(1)十字框中的五个数的和与中间的数16有什么关系?
(2)若将十字框上下左右移动,可框住另外的五个数,其他五个数的和能等于2010吗?如能,写出这五个数,如不能,说明理由.
【答案】(1)十字框中的五个数的和是中间的数16的5倍;(2)能;这五个数分别是:392、400、402、404、412.
【解析】
(1)将十字框中的五个数求和找到和与16的关系即可;
(2)设中间数为n,再用n分别表示出其它的四个数(竖着相邻两数差10,横着相邻两数差2),利用五个数的和列方程,若能求出偶数n,即五个数的和等于2010;若求出的n不是偶数,则不能.
解:(1)框中的五个数的和为:6+14+16+18+26=80,80是16的5倍,
故十字框中的五个数的和是中间的数16的5倍;
(2)能,
设中间数为n,则上边的数为(n-10),左边的数为(n-2),右边的数为(n+2),下边的数为(n+10),
∵五个数的和等于2010
∴(n-10)+(n-2)+n+(n+2)+(n+10)=2010
解得:n=402,符合题意,
则其它四个数分别为:392、400、404、412.
答:能,这五个数分别是:392、400、402、404、412

【题目】近几年,全社会对空气污染问题越来越重视,空气净化器的销量也在逐年增加.某商场从厂家购进了A,B两种型号的空气净化器,两种净化器的销售相关信息见下表:
A型销售数量(台) | B型销售数量(台) | 总利润(元) |
5 | 10 | 2 000 |
10 | 5 | 2 500 |
(1)每台A型空气净化器和B型空气净化器的销售利润分别是多少?
(2)该公司计划一次购进两种型号的空气净化器共100台,其中B型空气净化器的进货量不少于A型空气净化器的2倍,为使该公司销售完这100台空气净化器后的总利润最大,请你设计相应的进货方案;
(3)已知A型空气净化器的净化能力为300 m3/小时,B型空气净化器的净化能力为200 m3/小时.某长方体室内活动场地的总面积为200 m2,室内墙高3 m.该场地负责人计划购买5台空气净化器每天花费30分钟将室内空气净化一新,如不考虑空气对流等因素,至少要购买A型空气净化器多少台?