题目内容
【题目】已知平行四边形ABCD的对角线交于点O,点P是直线BD上任意一点(异于B、O、D三点),过P点作平行于AC的直线交直线AD于点E,交直线BA于点F,当点P在线段BD上时,易证得:AC=PE+PF(如图①所示).当点P在线段BD的延长线上(如图②所示)和当点P在线段DB的延长线上(如图③所示)两种情况时,探究线段AC、PE、PF之间的数量关系,并对图③的结论进行证明.
【答案】解:当P在BD的延长线上时,如图②,延长FE交BC的延长线于点G,
∵AC∥FG,
∴![]() ,
,
∵四边形ABCD为平行四边形,
∴AO=CO,
∴PF=PG,
∴EG=PG﹣PE=PF﹣PE,
又∵AB∥CG,AC∥EG,
∴四边形ACGE为平行四边形,
∴AC=EG,
∴AC=PF﹣PE;
当P在DB的延长线上时,如图③,延长CB交EF于点G,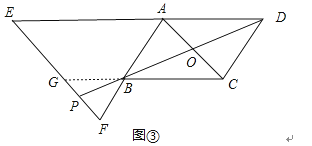
∵AC∥EF,
∴![]() ,
,
∵四边形ABCD为平行四边形,
∴AO=CO,
∴PG=PF,
∴EG=PE﹣PG=PE﹣PF,
又∵AC∥EG,AE∥CG,
∴四边形AEGC为平行四边形,
∴EG=AC,
∴AC=PE﹣PF.
【解析】在②中延长FE交BC的延长线于点G,可证得PF=PG,再证明四边形ACGE为平行四边形可得AC=EG,可得到AC=PF﹣PE;在③中延长CB交EF于点G,可证得PG=PF,可得到AC=PE﹣PF.
【考点精析】关于本题考查的平行四边形的性质,需要了解平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分才能得出正确答案.

练习册系列答案
相关题目
