题目内容
如图,已知AB∥CD,CE、AE分别平分∠ACD、∠CAB,则∠1+∠2______90°.(填“>”、“<”或“=”)
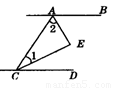
【答案】
=
【解析】
试题分析:由AB∥CD,根据两直线平行,同旁内角互补,可得∠BAC+∠ACD=180°,又由CE、AE分别平分∠ACD、∠CAB,可得∠1=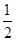 ∠BAC,∠2=
∠BAC,∠2=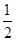 ∠ACD,则可求得∠1+∠2的度数.
∠ACD,则可求得∠1+∠2的度数.
∵AB∥CD,
∴∠BAC+∠ACD=180°,
∵CE、AE分别平分∠ACD、∠CAB,
∴∠1=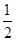 ∠BAC,∠2=
∠BAC,∠2=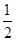 ∠ACD,
∠ACD,
∴∠1+∠2=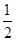 ∠BAC+
∠BAC+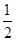 ∠ACD=
∠ACD=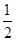 (∠BAC+∠ACD)=
(∠BAC+∠ACD)=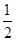 ×180°=90°.
×180°=90°.
考点:本题考查的是平行线的性质,角平分线的性质
点评:平行线的性质为:两直线平行同位角相等;两直线平行内错角相等;两直线平行同旁内角互补,熟练掌握平行线的性质是解本题的关键.在解答过程中还要具备整体意识。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
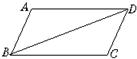 15、如图,已知AB=CD且∠ABD=∠BDC,要证∠A=∠C,判定△ABD≌△CDB的方法是( )
15、如图,已知AB=CD且∠ABD=∠BDC,要证∠A=∠C,判定△ABD≌△CDB的方法是( )
 如图,已知AB∥CD,∠1=50°25′,则∠2的大小是
如图,已知AB∥CD,∠1=50°25′,则∠2的大小是 如图,已知 AB∥CD,∠A=53°,则∠1的度数是
如图,已知 AB∥CD,∠A=53°,则∠1的度数是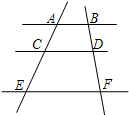 如图,已知AB∥CD∥EF,那么下列结论中,正确的是( )
如图,已知AB∥CD∥EF,那么下列结论中,正确的是( )