题目内容
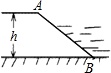如图，是一水库大坝横断面的一部分，坝高h=5m，近水斜坡AB=10m，则这个斜坡的坡度i=
| ||
| 3 |
| ||
| 3 |
分析：过点A作垂线构造直角三角形，利用勾股定理求得水平距离，再运用直角三角形三角函数求解．
解答：解：如图．过A作坝底的垂线，设垂足为C，得Rt△ABC，
在Rt△ABC中，AB=10m，AC=h=5m，
由勾股定理得：
BC=
=
=5
，
∴i=tanα=
=
=
，
故答案为：
．
在Rt△ABC中，AB=10m，AC=h=5m，
由勾股定理得：
BC=
| AB2-AC2 |
| 102-52 |
| 3 |
∴i=tanα=
| AC |
| BC |
| 5 | ||
5
|
| ||
| 3 |
故答案为：
| ||
| 3 |
点评：此题考查的知识点是解直角三角形的应用-坡度坡角问题，关键是构造直角三角形运用勾股定理和三角函数求解．
练习册系列答案
相关题目
；②用一组与背水坡面长边垂直的平行线将背水坡面分成9块相同的矩形区域，依次相间地种草与栽花．
；②用一组与背水坡面长边垂直的平行线将背水坡面分成9块相同的矩形区域，依次相间地种草与栽花．
