Question

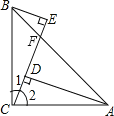
【题目】如图，∠ACB＝90°，AC＝BC，BE⊥CE于点E，AD⊥CE于点D，下面四个结论：①∠ABE＝∠BAD；②△CEB≌△ADC；③AB＝CE；④AD－BE＝DE.其中正确的结论是____.(把所有正确结论的序号都写在横线上)

Answer 1

【答案】①②④

【解析】

首先由△AEF与△ADF中分别有两个直角及对顶角得到①是正确的，利用等腰三角形的性质及其它条件，证明△CEB≌△ADC，则其他结论易求，而无法证明③是正确的．

如图，

∵∠BEF=∠ADF=90°，∠BFE=∠AFD，

∴①∠ABE=∠BAD，正确

∵∠1+∠2=90°∠2+∠CAD=90°，

∴∠1=∠CAD，

又∠E=∠ADC=90°，AC=BC，

∴②△CEB≌△ADC，正确

∴CE=AD，BE=CD，

∴④AD-BE=DE，正确

而③不能证明，

故答案为①、②、④．