题目内容
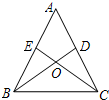 (2002•上海模拟)如图所示,下列条件中,不能推得△BOE≌△COD的是( )
(2002•上海模拟)如图所示,下列条件中,不能推得△BOE≌△COD的是( )分析:根据全等三角形全等的判定方法对各选项的条件进行分析判断后利用排除法求解.
解答:解:A、∵AB=AC,
∴∠ABC=∠ACB,
在△BCD和△CBE中,
,
∴△BCD≌△CBE(SAS),
∴∠BED=∠CDB,
在△BOE和△COD中,
,
∴△BOE≌△COD(AAS),故本选项错误;
B、∵AB=AC,OB=OC,
∴∠ABC=∠ACB,∠OBC=∠OCB,
∴∠ABC-∠OBC=∠ACB-∠OCB,
即∠EBO=∠DCO,
在△BOE和△COD中,
,
∴△BOE≌△COD(ASA),故本选项错误;
C、∵BE=CD,BD=CE,BC=BC(公共边),
∴△BCD≌△CBE(SSS),
∴∠BED=∠CDB,
在△BOE和△COD中,
,
∴△BOE≌△COD(AAS),故本选项错误;
D、BE=CD,OB=OC只能推出“边边角”的关系,无法证明得到△BOE≌△COD,故本选项正确.
故选D.
∴∠ABC=∠ACB,
在△BCD和△CBE中,
|
∴△BCD≌△CBE(SAS),
∴∠BED=∠CDB,
在△BOE和△COD中,
|
∴△BOE≌△COD(AAS),故本选项错误;
B、∵AB=AC,OB=OC,
∴∠ABC=∠ACB,∠OBC=∠OCB,
∴∠ABC-∠OBC=∠ACB-∠OCB,
即∠EBO=∠DCO,
在△BOE和△COD中,
|
∴△BOE≌△COD(ASA),故本选项错误;
C、∵BE=CD,BD=CE,BC=BC(公共边),
∴△BCD≌△CBE(SSS),
∴∠BED=∠CDB,
在△BOE和△COD中,
|
∴△BOE≌△COD(AAS),故本选项错误;
D、BE=CD,OB=OC只能推出“边边角”的关系,无法证明得到△BOE≌△COD,故本选项正确.
故选D.
点评:本题考查了全等三角形的判定,根据各选项的已知条件转化出△BOE和△COD全等的条件是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 (2002•上海模拟)如图,已知OABC为正方形,点A(-1,
(2002•上海模拟)如图,已知OABC为正方形,点A(-1,