题目内容
解答题:如图,⊙P与x轴相切于坐标原点O,⊙P与y轴交于点A(0,2),点B的坐标为(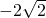 ,0),连接
,0),连接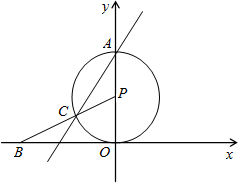 BP交⊙P于点C
BP交⊙P于点C
(1)求线段BC的长;
(2)求直线AC的函数解析式.
解:(1)∵⊙P与x轴切于坐标原点O,且交y轴于点A(0,2),
∴AO⊥x轴于O,OA是直径且OA=2,
∴OP=1,
又∵BP交⊙P于C,∴CP=1,
∵B(-2 ,0),∴OB=2
,0),∴OB=2 ,
,
Rt△BOP中,根据勾股定理得:BP=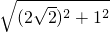 =3,
=3,
则BC=BP-CP=2;
(2)过C作CH⊥BO于H,
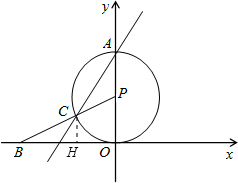
∵AO⊥x轴,
∴CH∥PO,
∴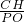 =
=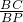 =
=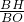 ,
,
又∵PO=1,BC=2,BP=3,OB=2 ,
,
∴CH=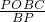 =
= ,BH=
,BH=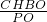 =
= ,
,
∴HO=OB-BH= ,
,
∴C(-
 ,
, ),
),
根据直线AC交y轴于点A(0,2),设直线AC的解析式为y=kx+2(k≠0),
将C的坐标代入得:-
 k+2=
k+2= ,
,
∴k= ,
,
∴直线AC的解析式为y= x+2.
x+2.
分析:(1)由圆P与x轴切于坐标原点,且与y轴交于A点,根据切线的性质得到AO垂直于x轴,且AO为直径,得到AO的长,由AO的长求出半径OP的长,再由PC为圆的半径,得出PC的长,同时由B的坐标得出OB的长,在三角形BOP中,由OP及OB的长,利用勾股定理求出BP的长,由BP-CP即可求出BC的长;
(2)过C作CH垂直于x轴,由AO也垂直于x轴,得到CH与AO平行,由平行得比例,列出比例式,将BO,PO,BC,BP的长代入,求出CH及BH的长,由OB-BH求出OH的长,根据CH及OH的长,得出C的坐标,由直线AC与y轴的交点A的坐标设出直线AC的方程为y=kx+2,k不为0,将C的坐标代入确定出k的值,即可确定出直线AC的解析式.
点评:此题属于一次函数的综合题,涉及的知识有:勾股定理,平行线的性质,利用待定系数法求一次函数的解析式,以及切线的性质,利用了数形结合及转化的数学思想,要求学生掌握知识要全面.
∴AO⊥x轴于O,OA是直径且OA=2,
∴OP=1,
又∵BP交⊙P于C,∴CP=1,
∵B(-2
 ,0),∴OB=2
,0),∴OB=2 ,
,Rt△BOP中,根据勾股定理得:BP=
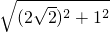 =3,
=3,则BC=BP-CP=2;
(2)过C作CH⊥BO于H,
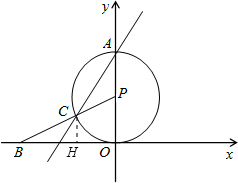
∵AO⊥x轴,
∴CH∥PO,
∴
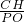 =
=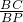 =
=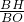 ,
,又∵PO=1,BC=2,BP=3,OB=2
 ,
,∴CH=
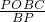 =
= ,BH=
,BH=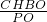 =
= ,
,∴HO=OB-BH=
 ,
,∴C(-

 ,
, ),
),根据直线AC交y轴于点A(0,2),设直线AC的解析式为y=kx+2(k≠0),
将C的坐标代入得:-

 k+2=
k+2= ,
,∴k=
 ,
,∴直线AC的解析式为y=
 x+2.
x+2.分析:(1)由圆P与x轴切于坐标原点,且与y轴交于A点,根据切线的性质得到AO垂直于x轴,且AO为直径,得到AO的长,由AO的长求出半径OP的长,再由PC为圆的半径,得出PC的长,同时由B的坐标得出OB的长,在三角形BOP中,由OP及OB的长,利用勾股定理求出BP的长,由BP-CP即可求出BC的长;
(2)过C作CH垂直于x轴,由AO也垂直于x轴,得到CH与AO平行,由平行得比例,列出比例式,将BO,PO,BC,BP的长代入,求出CH及BH的长,由OB-BH求出OH的长,根据CH及OH的长,得出C的坐标,由直线AC与y轴的交点A的坐标设出直线AC的方程为y=kx+2,k不为0,将C的坐标代入确定出k的值,即可确定出直线AC的解析式.
点评:此题属于一次函数的综合题,涉及的知识有:勾股定理,平行线的性质,利用待定系数法求一次函数的解析式,以及切线的性质,利用了数形结合及转化的数学思想,要求学生掌握知识要全面.

练习册系列答案
相关题目
 BP交⊙P于点C
BP交⊙P于点C

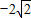 ,0),连接BP交⊙P于点C
,0),连接BP交⊙P于点C