题目内容
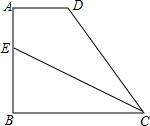 直角梯形ABCD中,AB⊥BC,AD∥BC,BC>AD,AD=2,AB=4,点E在AB上,将△CBE沿CE翻折,使B点与D点重合,则∠BCE的正切值是
直角梯形ABCD中,AB⊥BC,AD∥BC,BC>AD,AD=2,AB=4,点E在AB上,将△CBE沿CE翻折,使B点与D点重合,则∠BCE的正切值是分析:连接BD.根据折叠的性质,CE垂直平分BD.可证∠BCE=∠ABD,在△ABD中求出tan∠ABD得解.
解答: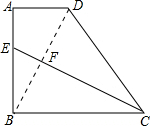 解:连接BD,交CE于点F.
解:连接BD,交CE于点F.
根据题意得CE⊥BD.
∵∠BCE+∠BEC=90°,∠BEC+∠EBF=90°,
∴∠BCE=∠ABD.
∵tan∠ABD=
=
=
,
∴tan∠BCE=
.
 解:连接BD,交CE于点F.
解:连接BD,交CE于点F.根据题意得CE⊥BD.
∵∠BCE+∠BEC=90°,∠BEC+∠EBF=90°,
∴∠BCE=∠ABD.
∵tan∠ABD=
| AD |
| AB |
| 2 |
| 4 |
| 1 |
| 2 |
∴tan∠BCE=
| 1 |
| 2 |
点评:本题考查图形的翻折变换,解题过程中应注意折叠是一种对称变换,它属于轴对称,根据轴对称的性质,折痕垂直平分对应点的连线.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
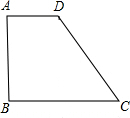 在直角梯形ABCD中,底AD=6cm,BC=11cm,腰CD=12cm,则这个直角梯形的周长为
在直角梯形ABCD中,底AD=6cm,BC=11cm,腰CD=12cm,则这个直角梯形的周长为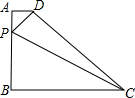 如图,直角梯形ABCD中,AD∥BC,∠B=90°,AD=1,BC=8,AB=6,点P在高AB上滑动,当AP长为
如图,直角梯形ABCD中,AD∥BC,∠B=90°,AD=1,BC=8,AB=6,点P在高AB上滑动,当AP长为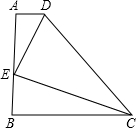 下结论:
下结论: EF∥AB,交AD于点E,CF=4cm.
EF∥AB,交AD于点E,CF=4cm.