题目内容
如图,AB为⊙O的直径,CD切⊙O于D,CD=AB,E为AB下方⊙O上一点,且

(1)求证:四边形ABCD是平行四边形(2)若⊙O半径为5,AE=8,求 的正切值
的正切值


(1)求证:四边形ABCD是平行四边形(2)若⊙O半径为5,AE=8,求
 的正切值
的正切值(1)见解析(2)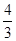
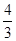
(1)连结OD, 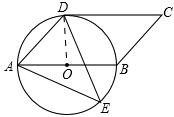
∵CD切⊙O于D, ∴OD⊥DC---------1分
∵∠AED=45° ∴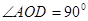 即DO⊥AB---------1分 ∴AB∥CD---------1分
即DO⊥AB---------1分 ∴AB∥CD---------1分
∵CD=AB ∴四边形ABCD是平行四边形---------1分
(2)连结BE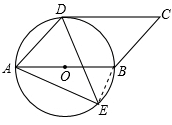
∵AB为⊙O的直径 ∴∠AEB=90°---------1分
∵⊙O的半径为5,AE=8 ∴BE=6-------1分 ∴tan∠ADE=tan∠ABE=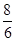
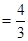 -----2分
-----2分
(1)连结OD,求得OD⊥DC,DO⊥AB,得出结论
(2) (2)连接BE,则∠ADE=∠ABE,由AB是⊙O的直径得到∠AEB=90°,而AB=2×3=6(cm).在Rt△ABE中,利用三角函数的定义即可求解

∵CD切⊙O于D, ∴OD⊥DC---------1分
∵∠AED=45° ∴
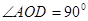 即DO⊥AB---------1分 ∴AB∥CD---------1分
即DO⊥AB---------1分 ∴AB∥CD---------1分 ∵CD=AB ∴四边形ABCD是平行四边形---------1分
(2)连结BE

∵AB为⊙O的直径 ∴∠AEB=90°---------1分
∵⊙O的半径为5,AE=8 ∴BE=6-------1分 ∴tan∠ADE=tan∠ABE=
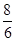
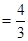 -----2分
-----2分(1)连结OD,求得OD⊥DC,DO⊥AB,得出结论
(2) (2)连接BE,则∠ADE=∠ABE,由AB是⊙O的直径得到∠AEB=90°,而AB=2×3=6(cm).在Rt△ABE中,利用三角函数的定义即可求解

练习册系列答案
相关题目

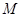 是⊙
是⊙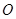 的直径
的直径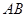 上任意一点,过点
上任意一点,过点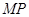 ,
,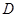 是
是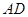 交⊙
交⊙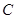 ,且
,且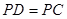 .
.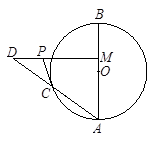
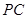 与⊙
与⊙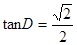 ,
,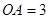 ,过点A作
,过点A作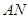 交⊙
交⊙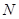 .求弦
.求弦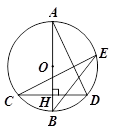

 的圆形纸片剪去
的圆形纸片剪去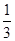 圆周的一个扇形,将留下在扇形围成一个圆锥(接缝处不重叠),那么这个圆锥的体积是__◆ .
圆周的一个扇形,将留下在扇形围成一个圆锥(接缝处不重叠),那么这个圆锥的体积是__◆ .
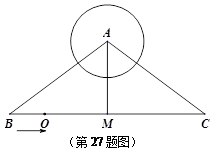
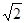 ,cosB=,求⊙O的半径.
,cosB=,求⊙O的半径.