题目内容
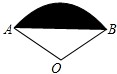
如图所示,扇形AOB的圆心角为120°,半径为2,则图中阴影部分的面积为( )
A.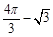 B.
B.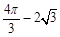 C.
C.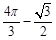 D.
D.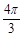
【答案】
A
【解析】
试题分析:作OD⊥AB于点D,根据垂径定理及勾股定理即可求得AD、OD的长,再由阴影部分的面积等于圆心角为120°的扇形的面积减去△AOB的面积即可求得结果.
作OD⊥AB于点D
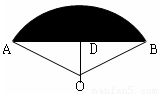
∵OA=OB=2,∠AOB=120°
∴∠OAB=30°
∴OD=1
∴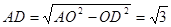
∴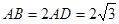
∴阴影部分的面积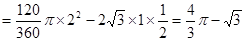
故选A.
考点:垂径定理,勾股定理,扇形的面积公式,三角形的面积公式
点评:解题的关键是熟练掌握扇形的面积公式: ,注意在使用公式时度不带单位.
,注意在使用公式时度不带单位.

练习册系列答案
相关题目
如图所示,扇形AOB的中心角为60°,半径为6,C、D分别是
的三等分点,则阴影部分的面积是( )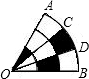
 |
| AB |

| A、16π | B、6π | C、2π | D、π |
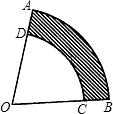 如图所示,扇形AOB中,∠AOB=60°,AD=3cm,
如图所示,扇形AOB中,∠AOB=60°,AD=3cm,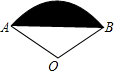 (2012•黄石)如图所示,扇形AOB的圆心角为120°,半径为2,则图中阴影部分的面积为( )
(2012•黄石)如图所示,扇形AOB的圆心角为120°,半径为2,则图中阴影部分的面积为( ) 如图所示,扇形AOB的圆心角为120°,半径为2,则图中阴影部分的面积为
如图所示,扇形AOB的圆心角为120°,半径为2,则图中阴影部分的面积为