题目内容
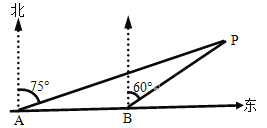
【题目】如图所示,为了躲避海盗,一轮船由西向东航行,早上8点,在A处测得小岛P在北偏东75°的方向上,以每小时20海里的速度继续向东航行,10点到达B处,并测得小岛P在北偏东60°的方向上,已知小岛周围22海里内有暗礁,若轮船仍向前航行,有无触礁的危险?
【答案】无触礁危险
【解析】
试题分析:过P作AB的垂线PD,在直角△BPD中可以求的∠PAD的度数是30度,即可证明△APB是等腰三角形,即可求得BP的长,进而在直角△BPD中,利用30度的锐角所对的直角边等于斜边的一半,从而求得PD的长,即可确定继续向东航行是否有触礁的危险,确定是否能一直向东航行.
试题解析:过点P作PC⊥AB于点C,∠PAB=15°,∠APB=15°,
∴BA=BP=2×20=40海里。
在Rt△PBC中,PC=![]() BP=20海里<22海里。
BP=20海里<22海里。
故,该船无触礁危险。

练习册系列答案
相关题目
