��Ŀ����
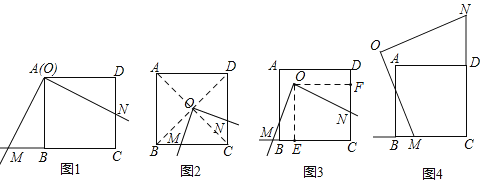
����Ŀ������������ABCD��һ����OΪֱ�Ƕ��������ǰ壬�ƶ����ǰ壬ʹ���ǰ����ֱ�DZ�����ֱ�߷ֱ���ֱ��BC��CD������M��N��
��1����ͼ1������O���A�غϣ���OM��ON��������ϵ��__________________��
��2����ͼ2������O�������ε����ģ������Խ��ߵĽ���������1���еĽ����Ƿ���Ȼ��������˵��������
��3����ͼ3������O�������ε��ڲ������߽�������OM=ONʱ����̽����O���ƶ������п��γ�ʲôͼ�Σ�
��4����ͼ4�ǵ�O���������ⲿ��һ���������OM=ONʱ������͡���O��λ���ڸ�������£����ⲿ���ƶ����γɵ�ͼ�Ρ����һ����ȷ�Ľ��ۣ�������˵����

���𰸡���1��OM=ON����2��OM=ON�Գ�������3����O���������ڣ����߽����ƶ����γɵ�ͼ���ǶԽ���AC����4�����γɵ�ͼ��Ϊֱ��AC��
��������
�����������1�����ݡ�OBM���ODNȫ�ȣ����Եó�OM��ON��ȵ�������ϵ��
��2������AC��BD����ͨ���ж���BOM�ա�CON�����Եõ�OM=ON��
��3������O��OE��BC����OF��CD������ͨ���ж���MOE�ա�NOF���ó�OE=OF���������ֵ�O�ڡ�C��ƽ�����ϣ�
��4���������ã�3�����������ߵķ������ж�������ȫ�Ȳ��ó����ۣ�
�����������1������O���A�غϣ���OM��ON��������ϵ�ǣ�OM=ON��
��2���Գ�����
֤������ͼ2������AC��BD��
��������ABCD�ɵã���BOC=90�㣬BO=CO����OBM=��OCN=45�㣮�ߡ�MON=90�������BOM=��CON���ڡ�BOM�͡�CON�����ߡ�OBM=��OCN��BO=CO����BOM=��CON�����BOM�ա�CON��ASA������OM=ON��
��3����ͼ3������O��OE��BC����OF��CD������ֱ�ΪE��F�����OEM=��OFN=90�����֡ߡ�C=90��������EOF=90��=��MON�����MOE=��NOF��
�ڡ�MOE�͡�NOF�����ߡ�OEM=��OFN����MOE=��NOF��OM=ON�����MOE�ա�NOF��AAS������OE=OF��
�֡�OE��BC��OF��CD�����O�ڡ�C��ƽ����������O���ƶ������п��γ��߶�AC��
��4��O���ƶ������п��γ�ֱ��AC��

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�