��Ŀ����
����Ŀ����ͼ��Rt��ABO����ֱ�DZ�OA��OB�ֱ���x��ĸ������y����������ϣ�OΪ����ԭ�㣬A��B���������ֱ�Ϊ��![]() ��0������0��4����������
��0������0��4����������![]() ����B�㣬�Ҷ�����ֱ��
����B�㣬�Ҷ�����ֱ��![]() �ϣ�
�ϣ�
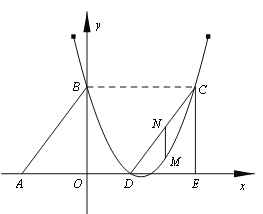
��1���������߶�Ӧ�ĺ�����ϵʽ��
��2������DCE���ɡ�ABO��x������ƽ�Ƶõ��ģ����ı���ABCD������ʱ�����жϵ�C�͵�D�Ƿ������������ϣ���˵�����ɣ�
��3����M����CD����ֱ���·����������ϵ�һ�����㣬����M��MNƽ����y�ύCD�ڵ�N�����M�ĺ�����Ϊt��MN�ij���Ϊl����l��t֮��ĺ�����ϵʽ������lȡ���ֵʱ����M�����꣮
���𰸡���1��y=![]() x2-
x2-![]() x+4����2����C�͵�D�������������ϣ���3����M������Ϊ��
x+4����2����C�͵�D�������������ϣ���3����M������Ϊ��![]() ��
��![]() ����
����
��������
�����������1����֪����������A��B��������Լ������ߵĶԳ��᷽�̣����ô���ϵ������������ߵĽ���ʽ��
��2���������AB�ij�����A��B����������ƽ��AB����λ�����ɵó�C��D�����꣬�ٴ��������ߵĽ���ʽ�н�����֤���ɣ�
��3������C��D�����꣬�����ֱ��CD�Ľ���ʽ����ô�߶�MN�ij�ʵ����ֱ��BC�������ߵĺ���ֵ�IJ�ɽ�x=t�������������Ľ���ʽ�У��ó���������ֵ�IJΪl�ı���ʽ���ɴ˿����l��t�ĺ�����ϵʽ���������ú��������ʼ������lȡ���ֵʱ����M�����꣮
�����������1����������y=![]() x2+bx+c�Ķ�����ֱ��x=
x2+bx+c�Ķ�����ֱ��x=![]() �ϣ�
�ϣ�
���������������߶�Ӧ�ĺ�����ϵʽΪy=![]() ��x-
��x-![]() ��2+m
��2+m
����B��0��4���ڴ��������ϣ�
��4=![]() ����-
����-![]() ��2+m
��2+m
��m=-![]()
����������ϵʽΪ��y=![]() ��x-
��x-![]() ��2-
��2-![]() =
=![]() x2-
x2-![]() x+4
x+4
��2����Rt��ABO��OA=3��OB=4��
��AB=![]() =5
=5
���ı���ABCD������
��BC=CD=DA=AB=5
��C��D���������ֱ��ǣ�5��4������2��0����
��x=5ʱ��y=![]() ��52-
��52-![]() ��5+4=4
��5+4=4
��x=2ʱ��y=![]() ��22-
��22-![]() ��2+4=0
��2+4=0
����C�͵�D�������������ϣ�
��3����ֱ��CD��Ӧ�ĺ�����ϵʽΪy=kx+b����
��![]() ��
��
��ã�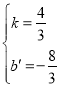 ��
��
��y=![]() x-
x-![]()
��MN��y�ᣬM��ĺ�����Ϊt��
��N��ĺ�����ҲΪt��
��yM=![]() t2-
t2-![]() t+4��yN=
t+4��yN=![]() t-
t-![]() ��
��
��l=yN-yM=![]() t-
t-![]() -��
-��![]() t2-
t2-![]() t+4��=-
t+4��=-![]() t2+
t2+![]() t-
t-![]() =-
=-![]() ��t-
��t-![]() ��2+
��2+![]()
��-![]() ��0��
��0��
����t=![]() ʱ��l���=
ʱ��l���=![]() ��yM=
��yM=![]() t2-
t2-![]() t+4=
t+4=![]() ��
��
��ʱ��M������Ϊ��![]() ��
��![]() ����
����

 ��У����ϵ�д�
��У����ϵ�д�