题目内容
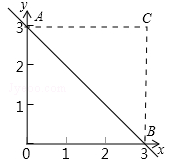
 14、如图,以O为坐标原点,OB、OA分别在x轴、y轴上,点A的坐标为(0,3),点B坐标为(3,0),将△AOB沿AB折叠,点O落在点C处,则点C的坐标是
14、如图,以O为坐标原点,OB、OA分别在x轴、y轴上,点A的坐标为(0,3),点B坐标为(3,0),将△AOB沿AB折叠,点O落在点C处,则点C的坐标是(3,3)
.分析:根据点A的坐标为(0,3),点B坐标为(3,0),得OA=OB;根据折叠,得OA=AC,BC=OB,结合∠AOB=90°,即可证明四边形OABC是正方形,从而求得点C的坐标.
解答:解:∵点A的坐标为(0,3),点B坐标为(3,0),
∴OA=OB=3.
根据折叠,得OA=AC,BC=OB,
又∠AOB=90°,
∴四边形OABC是正方形.
∴∠OAC=90°,AC=OA=3.
即点C(3,3).
∴OA=OB=3.
根据折叠,得OA=AC,BC=OB,
又∠AOB=90°,
∴四边形OABC是正方形.
∴∠OAC=90°,AC=OA=3.
即点C(3,3).
点评:根据折叠的性质和正方形的判定,可以得到四边形OABC是正方形,从而求得点C的坐标.

练习册系列答案
相关题目
 18、如图,这是某市部分简图,
18、如图,这是某市部分简图,
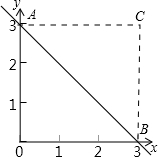 如图,以O为坐标原点,OB、OA分别在x轴、y轴上,点A的坐标为(0,3),点B坐标为(3,0),将△AOB沿AB折叠,点O落在点C处,则点C的坐标是________.
如图,以O为坐标原点,OB、OA分别在x轴、y轴上,点A的坐标为(0,3),点B坐标为(3,0),将△AOB沿AB折叠,点O落在点C处,则点C的坐标是________.