题目内容
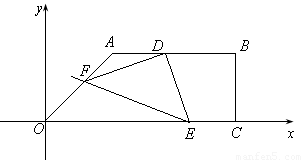
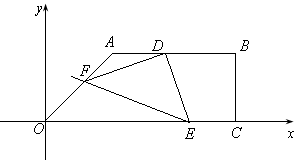
如图,面积为39的直角梯形OABC的直角顶点C在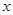 轴上,点C坐标为
轴上,点C坐标为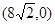 ,AB=
,AB=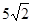 ,点D是AB边上的一点,且AD:BD=2︰3.有一45°的角的顶点E在
,点D是AB边上的一点,且AD:BD=2︰3.有一45°的角的顶点E在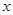 轴上运动,角的一边过点D,角的另一边与直线OA交于点F(点D、E、F按顺时针排列),连结DF.设CE=
轴上运动,角的一边过点D,角的另一边与直线OA交于点F(点D、E、F按顺时针排列),连结DF.设CE=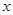 ,OF=
,OF=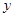 .
.
(1)求点D的坐标及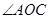 的度数;
的度数;
(2)若点E在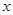 轴正半轴上运动,求
轴正半轴上运动,求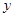 与
与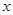 的函数关系式;
的函数关系式;
(3)在点E的运动过程中,是否存在某一时刻,使得△DEF成为等腰三角形?若存在,请求出所有符合条件的点F的坐标;若不存在,请说明理由.
(1)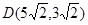
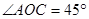 (2)
(2)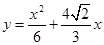 (3) 存在,理由见解析
(3) 存在,理由见解析
【解析】(1)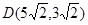
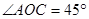 (1个对2分;2个对3分) …………………3分
(1个对2分;2个对3分) …………………3分
(2)当E在OC上时,如图,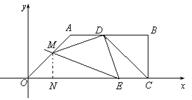
可得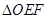 ∽
∽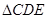 ……………………………4分
……………………………4分
∴ 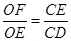 即
即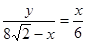 …………5分
…………5分
∴ 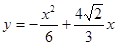 ……………………6分
……………………6分
当E在C的右侧上时,如图,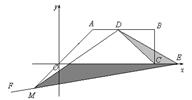
可得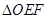 ∽
∽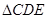
∴ 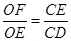 即
即 ∴
∴ 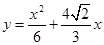 ……………………7分
……………………7分
(3)当E在OC上时,如图,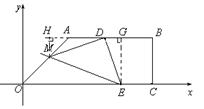
若EM=ED,则 ≌
≌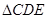
∴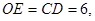
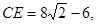
∴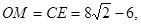 作
作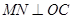 于点N
于点N
∴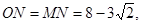
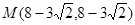
若DM=DE,则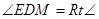 ,如图
,如图
作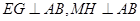 ,则
,则 ≌
≌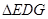
∴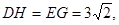
∴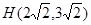 ,
,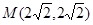
若MD=ME,则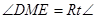 ,如图
,如图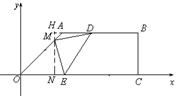
过M作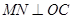 于点N交直线AB于点H,可得
于点N交直线AB于点H,可得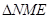 ≌
≌
设ON=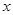 ,则MN=
,则MN=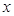 ,
MH=
,
MH=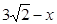 ,DH=
,DH=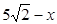
由MN=DH得: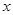 =
=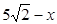 ,
,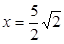 ∴
∴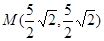
当E在C的右侧时,如图,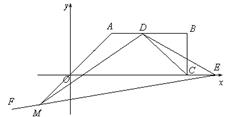
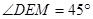 ,
,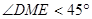 ,
,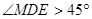
∴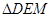 不可能是等腰三角形
不可能是等腰三角形
当E在O的左侧时,如图,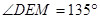
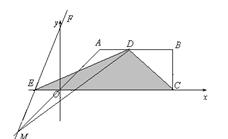
∴ 只能EM=ED,此时 ≌
≌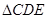
∴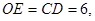
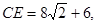
∴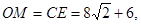 ∴
∴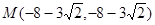
综合得: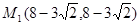 ,
,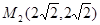 ,
,
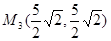 ,
,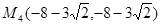 …………………………12分
…………………………12分
(第一个正确答案得2分,以后每对一个得1分)
(1)根据直角梯形的面积求得B点坐标,通过AD:BD=2︰3,求得点D的坐标,过A作OC的垂线,垂足为G,可求得AG=OG,从而得出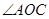 的度数
的度数
(2)分两种情况讨论,当E在OC上时,当E在C的右侧上时,通过相似三角形可求得 与
与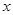 的函数关系式
的函数关系式
(3)当E在OC上时,由三种可能:EM=ED、DM=DE、MD=ME;当E在C的右侧时,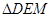 不可能是等腰三角形,当E在O的左侧时,只能EM=ED时,使得△DEF成为等腰三角形
不可能是等腰三角形,当E在O的左侧时,只能EM=ED时,使得△DEF成为等腰三角形

 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 OA交于点F(点D、E、F按顺时针排列),连接DF.设CE=x,OF=y.
OA交于点F(点D、E、F按顺时针排列),连接DF.设CE=x,OF=y.
 轴上,点C坐标为
轴上,点C坐标为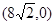 ,AB=
,AB=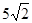 ,点D是AB边上的一点,且AD:BD=2︰3.有一45°的角的顶点E在
,点D是AB边上的一点,且AD:BD=2︰3.有一45°的角的顶点E在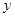 .
.
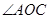 的度数;
的度数; 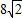 ,0),AB=
,0),AB=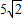 ,点D是AB边上的一点,且AD:BD=2:3.有一45°的角的顶点E在x轴上运动,角的一边过点D,角的另一边与直线
,点D是AB边上的一点,且AD:BD=2:3.有一45°的角的顶点E在x轴上运动,角的一边过点D,角的另一边与直线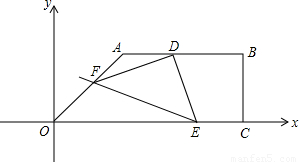 OA交于点F(点D、E、F按顺时针排列),连接DF.设CE=x,OF=y.
OA交于点F(点D、E、F按顺时针排列),连接DF.设CE=x,OF=y.