题目内容
（2007•乌鲁木齐）已知开口向上的抛物线y=ax2-2x+|a|-4经过点（0，-3）．
（1）此抛物线的解析式为
（2）当x=
（1）此抛物线的解析式为
y=x2-2x-3
y=x2-2x-3
；（2）当x=
1
1
时，y有最小值，这个最小值是-4
-4
．分析：（1）因为开口向上，所以a＞0；把点（0，-3）代入抛物线y=ax2-2x+|a|-4中，得|a|-4=-3，
再根据a＞0求a，从而确定抛物线解析式；
（2）根据二次函数的顶点坐标，求解即可．
再根据a＞0求a，从而确定抛物线解析式；
（2）根据二次函数的顶点坐标，求解即可．
解答：解：（1）由抛物线过（0，-3），得：
-3=|a|-4，
|a|=1，即a=±1．
∵抛物线开口向上，
∴a=1，
故抛物线的解析式为y=x2-2x-3；
（2）∵y=x2-2x-3=（x-1）2-4，
∴当x=1时，y有最小值-4．
-3=|a|-4，
|a|=1，即a=±1．
∵抛物线开口向上，
∴a=1，
故抛物线的解析式为y=x2-2x-3；
（2）∵y=x2-2x-3=（x-1）2-4，
∴当x=1时，y有最小值-4．
点评：此题考查了二次函数的开口方向，顶点坐标，还考查了点与函数的关系．
练习册系列答案
相关题目
，BC∥y轴且与x轴交于点C，直线OB与直线AC相交于点P．
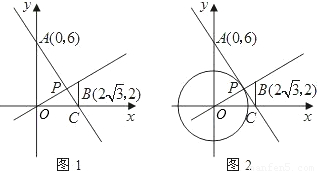
（k为常数，k≠0）的图象经过点（3，-4），则下列各点在该函数图象上的是（ ）