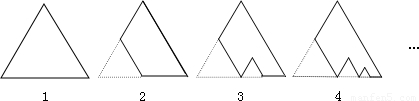
题目内容
如图,图1是一块边长为1,面积记为S1的正三角形纸板,沿图1的底边剪去一块边长为| 1 |
| 2 |
| 1 |
| 2 |
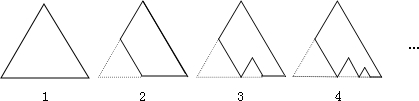
分析:根据等边三角形的性质得出,三角形的边长分别为:
,
,
…即相邻三角形相似比为:1:2,进而求出即相邻三角形面积比,从而得出规律.
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 8 |
解答:解:∵依次剪去一块更小的正三角形纸板,即其边长为前一块被剪掉正三角形纸板边长的
,
∴三角形的边长分别为:
,
,
…
即相邻三角形相似比为:1:2,
∴即相邻三角形面积比为:1:4,
∴剪去一块的正三角形纸板面积分别为:
,
,
,
…
第n个三角形的面积为:
,
故答案为:
.
| 1 |
| 2 |
∴三角形的边长分别为:
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 8 |
即相邻三角形相似比为:1:2,
∴即相邻三角形面积比为:1:4,
∴剪去一块的正三角形纸板面积分别为:
| ||
| 4 |
| ||
| 16 |
| ||
| 64 |
| ||
| 256 |
第n个三角形的面积为:
| ||
| 22n |
故答案为:
| ||
| 22n |
点评:此题主要考查了等边三角形的性质与数据的规律性知识,此题得出相邻三角形面积比,从而表示出各三角形面积是解决问题的关键.

练习册系列答案
 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目
 的正三角形纸板后得到图2,然后沿同一底边依次剪去一块更小的正三角形纸板(即其边长为前一块被剪掉正三角形纸板边长的
的正三角形纸板后得到图2,然后沿同一底边依次剪去一块更小的正三角形纸板(即其边长为前一块被剪掉正三角形纸板边长的 )后,得图3,4,…,记第n(n≥3)块纸板的面积为Sn,则Sn= .
)后,得图3,4,…,记第n(n≥3)块纸板的面积为Sn,则Sn= .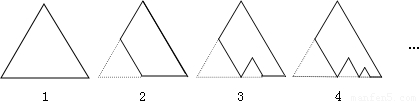
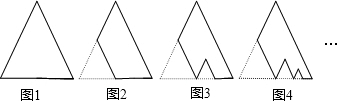
 的正三角形纸板后得到图2,然后沿同一底边依次剪去一块更小的正三角形纸板(即其边长为前一块被剪掉正三角形纸板边长的
的正三角形纸板后得到图2,然后沿同一底边依次剪去一块更小的正三角形纸板(即其边长为前一块被剪掉正三角形纸板边长的 )后,得图3,图4,…,记第n(n≥3)块纸板的面积为Sn,则Sn= .
)后,得图3,图4,…,记第n(n≥3)块纸板的面积为Sn,则Sn= .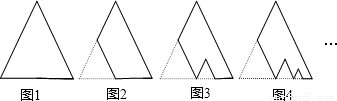
 的正三角形纸板后得到图2,然后沿同一底边依次剪去一块更小的正三角形纸板(即其边长为前一块被剪掉正三角形纸板边长的
的正三角形纸板后得到图2,然后沿同一底边依次剪去一块更小的正三角形纸板(即其边长为前一块被剪掉正三角形纸板边长的 )后,得图3,4,…,记第n(n≥3)块纸板的面积为Sn,则Sn= .
)后,得图3,4,…,记第n(n≥3)块纸板的面积为Sn,则Sn= .