题目内容
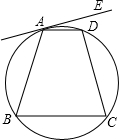（2012•台湾）如图所示的直线AE与四边形ABCD的外接圆相切于A点．若∠DAE=12°， |
| AB |
|
| BC |
|
| CD |
分析：作直径AF，连接DF，根据切线的性质求出∠F的度数，求出弧AD的度数，求出DC的度数，得出弧ADC的度数，即可求出答案．
解答：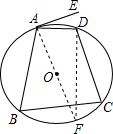
解：作直径AF，连接DF，
∵AE是⊙O的切线，
∴∠EAF=90°，
∵∠ADF=90°，
∴∠EAD+∠DAF=90°，∠F+∠DAF=90°，
∴∠F=∠DAE
∵∠DAE=12°（已知），
∴∠F=12°，
∴弧AD的度数是2×12°=24°，
∴
、
、
三弧的度数相等，
∴弧CD的度数是
×（360°-24°）=112°，
∴弧ADC的度数是24°+112°=136°，
∴∠ABC=
×136°=68°，
故选D．
解：作直径AF，连接DF，∵AE是⊙O的切线，
∴∠EAF=90°，
∵∠ADF=90°，
∴∠EAD+∠DAF=90°，∠F+∠DAF=90°，
∴∠F=∠DAE
∵∠DAE=12°（已知），
∴∠F=12°，
∴弧AD的度数是2×12°=24°，
∴
|
| AB |
|
| BC |
|
| CD |
∴弧CD的度数是
| 1 |
| 3 |
∴弧ADC的度数是24°+112°=136°，
∴∠ABC=
| 1 |
| 2 |
故选D．
点评：本题考查了切线的性质的应用，能求出弧AD的度数是解此题的关键，弦切角等于该弦所夹弧所对的圆周角，主要培养学生运用性质进行推理和计算的能力．
练习册系列答案
相关题目
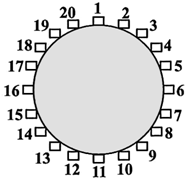（2012•台湾）如图，一圆桌周围有20个箱子，依顺时针方向编号1～20．小明在1号箱子中丢入一颗红球后，沿着圆桌依顺时针方向行走，每经过一个箱子就依下列规则丢入一颗球：
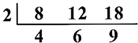（2012•台湾）如图是利用短除法求出三数8、12、18的最大公因子的过程．利用短除法，求出这三数的最小公倍数为何？（ ）
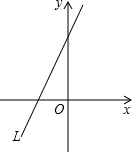（2012•台湾）如图，坐标平面上直线L的方程式为3x-y=-3．若有一直线L′的方程式为y=a，则a的值在下列哪一个范围时，L′与L的交点会在第二象限？（ ）
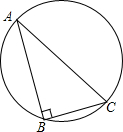（2012•台湾）如图，直角三角形ABC有一外接圆，其中∠B=90°，AB＞BC，今欲在