题目内容
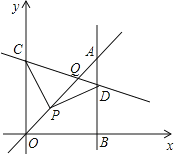
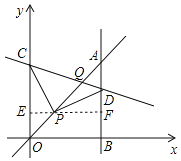
【题目】如图,平面直角坐标系中,已知点![]() ,C为y轴正半轴上一点,连接PC,线段PC绕点P顺时针旋转
,C为y轴正半轴上一点,连接PC,线段PC绕点P顺时针旋转![]() 至线段PD,过点D作直线
至线段PD,过点D作直线![]() 轴,垂足为B,直线AB与直线OP交于点A,且
轴,垂足为B,直线AB与直线OP交于点A,且![]() ,直线CD与直线OP交于点Q,则点Q的坐标为______.
,直线CD与直线OP交于点Q,则点Q的坐标为______.
【答案】![]()
【解析】
过点P作![]() 于E,EP的延长线交AB于F.首先证明△CPE≌△PDF,得到DF=PE=2,推出BD=BF+DF=4,由BD=4AD,推出AD=1,AB=OB=5,CE=PF=3,D(5,4),C(0,5),利用待定系数法求出直线CD的解析式,利用方程组即可求出点Q的坐标.
于E,EP的延长线交AB于F.首先证明△CPE≌△PDF,得到DF=PE=2,推出BD=BF+DF=4,由BD=4AD,推出AD=1,AB=OB=5,CE=PF=3,D(5,4),C(0,5),利用待定系数法求出直线CD的解析式,利用方程组即可求出点Q的坐标.
解:过点P作![]() 于E,EP的延长线交AB于F.
于E,EP的延长线交AB于F.
∵![]()
∴![]() ,
,
∴ 四边形EOBF是矩形,
∵ P (2,2)
∴ OE=PE=BF=2,
∵ ![]() ,
,
∴ ![]() ,
,![]() ,
,
∴ ![]() ,
,
在△CPE和△PDF中,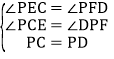 ,
,
∴ △CPE≌△PDF,
∴ DF=PE=2,
∴ BD=BF+DF =4,
∵ BD=4AD,
∴ AD=1,AB=OB=5,
∴ CE=PF=3,
∴ D(5,4),C(0,5),
设直线CD的解析式为y=kx+b则有![]() ,解得
,解得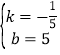 ,
,
∴直线CD的解析式为![]() ,
,
由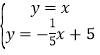 解得
解得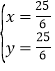 ,
,
∴点Q的坐标为![]() .
.
故答案为:![]() .
.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案 名题金卷系列答案
名题金卷系列答案
相关题目