题目内容
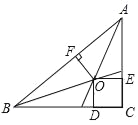
【题目】如图,在△ABC中,∠C=90°,O为△ABC的三条角平分线的交点,OD⊥BC,OE⊥AC,OF⊥AB,点D、E、F分别是垂足,且BC=8cm,CA=6cm,则点O到边AB的距离为( )
A. 2cm B. 3cm C. 4cm D. 5cm
【答案】A
【解析】
根据角平分线的性质得到OE=OF=OD,设OE=x,然后利用三角形面积公式得到S△ABC=S△OAB+S△OAC+S△OCB,于是可得到关于x的方程,从而可得到OF的长度.
在△ABC中,∵∠C=90°,BC=8cm,CA=6cm,∴AB=10cm.
∵点O为△ABC的三条角平分线的交点,∴OE=OF=OD,设OE=x.
∵S△ABC=S△OAB+S△OAC+S△OCB,∴![]() ×6×8=
×6×8=![]() OF×10+
OF×10+![]() OE×6+
OE×6+![]() OD×8,∴5x+3x+4x=24,∴x=2,∴点O到AB的距离等于2.
OD×8,∴5x+3x+4x=24,∴x=2,∴点O到AB的距离等于2.
故选A.

练习册系列答案
相关题目